Numerieke Wiskunde: verschil tussen versies
k Spellingspolitie kan zelf niet spellen |
Geen bewerkingssamenvatting |
||
| (261 tussenliggende versies door 92 gebruikers niet weergegeven) | |||
| Regel 1: | Regel 1: | ||
= | [[Afbeelding:MarcVanBarel.jpg|right|200px|]] | ||
= Didactisch Team = | |||
{| | |||
! Academiejaar | |||
! Professor(en) | |||
! Assistent(en) | |||
|- | |||
| 2019-2020 | |||
| Professor1, Professor2 | |||
| Assistent1, Assistent2 | |||
|- | |||
| 2020-2021 | |||
| Professor1, Professor2 | |||
| Assistent1, Assistent2 | |||
|} | |||
=Samenvattingen= | |||
[[Numerieke Wiskunde/Samenvattingen| Klik hier om de samenvattingen te bekijken]] | |||
Korte samenvatting + enkele oplossingen Dries 2018-2019: [https://drive.google.com/drive/folders/1jWKoYH4Y7uo5qMxcXJZsihP5P_6S7bPN?usp=sharing google drive map] | |||
=Het examen= | |||
'''2021-2021''': Examen van prof. Van Barel. Door corona duurde het examen 3 uur en bestond het examen uit 3 vragen. Het bericht van de prof op Toledo onder '2018-2019' geldt ook dit jaar. De vragen kwamen bijna exact overeen met vragen 1, 5 en 6 van het voorbeeldexamen onderaan de pagina. | |||
'''Vraag 1:''' Gegeven een bepaalde functie, bespreek de conditie en de stabiliteit. | |||
'''Vraag 2:''' Gegeven een kwadratuurformule, bepaal de gewichten zodat de nauwkeurigheidsgraad zo hoog mogelijk ligt. Wat is de | |||
nauwkeurigheidsgraad? | |||
'''Vraag 3:''' Gegeven een matrix en een grafiek (semilogy) van de relatieve fout met respect tot het aantal uitgevoerde stappen. | |||
Verklaar de grafiek (redelijke vage vraag). Bereken convergentieorde en convergentiefactor. Bepaal orde en factor grafisch. Komt dit | |||
overeen met je antwoord uit vraag b? | |||
'''2018-2019''': Het examen was uitzonderlijk schriftelijk omdat Marc Van Barel wegens medische redenen een groot deel van het semester afwezig was. Het examen was dan ook als een schriftelijk examen opgesteld, waardoor de vragen misschien niet erg representatief zijn voor de vragen mét mondelinge toelichting. Wel is het nog steeds open boek, al is het niet meer 'all you can carry' zoals het voorheen was ''(zie bericht toledo onderaan)''. Het examen bestond uit een opgavebundel, waarna je de vragen (sommigen met een lengte/regel-restrictie) op blanco papier moest oplossen. Het examen duurde in totaal 4 uur. | |||
Bericht van de prof op Toledo: ''Het examen is open-boek in de volgende betekenis: Het handboek, de tekst ivm splines en de slides alsook een afdruk van de illustraties (o.a. jupyter notebooks) mogen op het examen gebruikt worden waarbij er hier en daar iets mag bijgeschreven worden ter verduidelijking. Opgaven van oefeningen en oplossingen mogen NIET gebruikt worden.'' | |||
=Vakevaluatie= | |||
''Elk puntje hieronder is iemands mening. Verander aub geen puntjes. Als je een andere mening hebt, gelieve ze onderaan toe te voegen.'' | |||
=====Kwaliteit cursus (prijs, duidelijkheid, overeenkomst met les, ...)===== | |||
* 2017: Handgeschreven "slides" en een handboek. Uiteindelijk moet je enkel de essentie kennen, en die staat in de slides. | |||
=====Studiebelasting (aantal studiepunten in verhouding met bestede tijd)===== | |||
* 2017: Zeventien oefenzittingen. Zeventien. Er is ook een practicum waarvoor je meer dan een semester de tijd krijgt. Als je het werk kunt spreiden, is dat zeker te doen. Tijdens de blok is het niet meer werk dan andere vakken van 6 sp. | |||
* 2022: Practicum kregen we dit jaar een dikke maand voor, dit is voldoende als je er genoeg aan werkt tijdens de paasvakantie anders kan het wel wat krapper worden. | |||
=====Plaats binnen de opleiding (nodige voorkennis, overlap met andere vakken, relevantie van het vak,...)===== | |||
* 2017: Volgens de informatici is het meer een wiskundevak. Volgens de wiskundigen is het meer een informaticavak. Zorg dat je BVP, lineaire algebra en calculus/wiskunde I eerst gevolgd hebt. | |||
* 2021: Dit vak is eerder een ingenieursvak en is niet heel nuttig voor wiskundigen. Voor informatici kan het wel nuttig zijn aangezien dit een mogelijk onderzoeksdomein is in de master computerwetenschappen. | |||
=====Manier van lesgeven bij hoorcolleges (snelheid, verstaanbaarheid, structuur, nut, ...)===== | |||
* 2017: De meesten zijn niet wild van de uitleg van Marc Van Barel. | |||
* 2019: De uitleg van Marc Van Barel is nog steeds niet geweldig, maar de assistent die overpakte vanaf les 3 of 4 was pakken beter. | |||
* 2022: De uitleg is nog altijd niet beter. | |||
=====Evaluatie oefenzittingen/labo's (nut, begeleiding, ...)===== | |||
* 2017: De oefenzittingen zijn niet echt noodzakelijk. | |||
* 2022: De oefenzittingen zijn nuttig (als je een goede assistent hebt) als je niet echt mee bent met de uitleg van de prof. | |||
=====Examen (mate waarin het een weerspiegeling is van de cursus, examenvorm, ...)===== | |||
* 2017: Je moet eigenlijk alleen de essentie begrijpen. Dat zeggen de assistenten ook herhaaldelijk. Je mag alles meenemen wat je wilt, dus sommigen profiteren hiervan door [https://github.com/NorfairKing/all-you-can-carry dit beest]af te drukken. | |||
* 2018: Het examen is niet langer open-boek zoals vorig jaar. Bericht van de prof op Toledo: ''Het examen is open-boek in de volgende betekenis: Het handboek, de tekst ivm splines en de slides alsook een afdruk van de illustraties (o.a. jupyter notebooks) mogen op het examen gebruikt worden waarbij er hier en daar iets mag bijgeschreven worden ter verduidelijking. Opgaven van oefeningen en oplossingen mogen NIET gebruikt worden.'' | |||
= Extra oefenmateriaal = | |||
Deze oefeningen zijn afkomstig van de website van de burgerlijk ingenieurs. | |||
http://examens.wina.be/images/Oefeningen_Burgies.doc | |||
Verder is hier een oud document dat ik nog terugvond. Het bevat opmerkingen en hulp bij de toenmalige oefenzittingen. (kan zijn dat die ondertussen wat veranderd zijn) De opmaak is verre van geslaagd, de EPS plots zitten er niet meer in, en het delta symbool is een lege verzameling symbool geworden. Voor wie het toch nog wil kan het wel een hulp zijn: [[Media:OefenzittingenNW.pdf]]. | |||
= Losse examenvragen = | |||
Git met oplossingen: https://github.com/KULeuven-CS/Numerieke-Wiskunde | |||
'''Hieronder een aantal examenvragen die van een aantal bronnen zijn samengeraapt...'''<br> | '''Hieronder een aantal examenvragen die van een aantal bronnen zijn samengeraapt...'''<br> | ||
| Regel 5: | Regel 76: | ||
'''De opmaak is niet altijd helemaal in orde''' | '''De opmaak is niet altijd helemaal in orde''' | ||
Hulp met wiskundesyntax vindt je hier: http://meta.wikimedia.org/wiki/Help:Formula | |||
Geachte heer Van Barel heeft de neiging om deze vragen letterlijk opnieuw te vragen, zie maar dat ge deze kent dus! <small>Maar wie de rest niet leert is nog dommer dan Jos Ghysen, en 't is niet omdat hij een tv programma gehad heeft dat gij dat ook zult hebben! Leren dus!.</small> Oppassen voor bijvragen (if any). <small>Maar in het jaar 2007 was dat toch niet meer waar, van die vragen opnieuw gesteld te hebben, dus zeker gewoon helemaal leren</small> | |||
Geldt nog steeds in het jaar 2007 hoor, je moet gewoon wat geluk hebben. En in 2008 was het weer zo dus maak alles wat hieronder staat maar! | |||
=== Examenvraag 1 === | === Examenvraag 1 === | ||
| Regel 31: | Regel 98: | ||
Verklaar waarom het verschil plots niet meer gelijk is aan 0. Waarvoor staat dat getal?<br> | Verklaar waarom het verschil plots niet meer gelijk is aan 0. Waarvoor staat dat getal?<br> | ||
=== Examenvraag 2 === | === Examenvraag 2 === | ||
Je krijgt de QR ontbinding van een matrix A, en Q'.b.<br> | Je krijgt de QR ontbinding van een matrix A, en Q'.b.<br> | ||
gevraagd: ||r|| en hoe zou je x bepalen dat hoort bij die ||r||.<br> | gevraagd: ||r|| en hoe zou je x bepalen dat hoort bij die ||r||.<br> | ||
=== Examenvraag 3 === | === Examenvraag 3 === | ||
Je krijgt een paar grafiekjes en maple code over Newton | Je krijgt een paar grafiekjes en maple code over Newton Raphson en de vereenvoudigde Newton Raphson (niet lineaire stelsels). Je krijgt een viertal kleine "verklaar waarom" vraagjes. | ||
=== Examenvraag 4 === | === Examenvraag 4 === | ||
Maple afdruk: laatste vraag van de examenvragen in de winabundel (Die over het bepalen van eigenwaarden met de methode van de machten). | Maple afdruk: laatste vraag van de examenvragen in de winabundel (Die over het bepalen van eigenwaarden met de methode van de machten). | ||
Uit de matrix A = [2 1 -1; 0 3 -5; 0 0 -2] wordt de dominante eigenwaarde berekend. De startwaarden zijn: [-1.00001 1.00002 1]. Op de grafiek is zichtbaar dat er eerst naar 2 lijkt te convergeren, maar uiteindelijk toch de juiste eigenwaarde 3 gekozen wordt. Het berekenen | Uit de matrix A = [2 1 -1; 0 3 -5; 0 0 -2] wordt de dominante eigenwaarde berekend. De startwaarden zijn: [-1.00001 1.00002 1]. Op de grafiek is zichtbaar dat er eerst naar 2 lijkt te convergeren, maar uiteindelijk toch de juiste eigenwaarde 3 gekozen wordt. Het berekenen gebeurt met de methode van de machten met normalisatie. | ||
* Hoe komt het dat er eerst naar 2 geconvergeerd wordt? | * Hoe komt het dat er eerst naar 2 geconvergeerd wordt? | ||
* Waarom uiteindelijk toch naar 3? | * Waarom uiteindelijk toch naar 3? | ||
* Wat als er geen normalisatie gebruikt zou worden? | * Wat als er geen normalisatie gebruikt zou worden? | ||
=== Examenvraag 5 === | === Examenvraag 5 === | ||
Maple printout<br> | Maple printout<br> | ||
<math>p_1=(x-2)(x-4)... (x-30)=\prod_{i = 1}^{15}(x-2i) </math><br> | |||
p_2 is p_1 uitgewerkt (geëxpandeerd): <math>p_2 = x^{15}+b_{14}x^{14}+...+b_0=\sum_{i=0}^{15}b_i x^i</math> [met b_i gegeven constanten, elke bi heeft een mantisse met precisie 10]<br> | |||
die twee geplot.<br> | die twee geplot.<br> | ||
| Regel 85: | Regel 128: | ||
#Maple code om te testen | #Maple code om te testen | ||
f:= (x-2 | Digits := 10; | ||
f:= product((x-2.0*i),i=1..15); | |||
g:=collect(f,x); | g:=collect(f,x); | ||
plot([f,g],x=2..6); | |||
plot([f,g],x=6..20); | |||
plot([f,g],x=20..30); | |||
De vraag is hoe het komt dat de fouten groter zijn voor grotere nulpunten. Als bijvraag moest ik verklaren waarom de fout voor vb. x=28 van de orde 10^13 is en van welke orde de fout dan is voor x = 4. ( dat laatste zag je niet op de grafiek, omdat de fout heel klein was tegenover de grootte van de functie zelf ). | De vraag is hoe het komt dat de fouten groter zijn voor grotere nulpunten. Als bijvraag moest ik verklaren waarom de fout voor vb. x=28 van de orde 10^13 is en van welke orde de fout dan is voor x = 4. ( dat laatste zag je niet op de grafiek, omdat de fout heel klein was tegenover de grootte van de functie zelf ). | ||
=== Examenvraag 6 === | === Examenvraag 6 === | ||
| Regel 107: | Regel 147: | ||
Gegeven dat alle gedeelde differenties van de vierde graad 1 zijn.<br> | Gegeven dat alle gedeelde differenties van de vierde graad 1 zijn.<br> | ||
Geef a3.<br> | Geef a3.<br> | ||
=== Examenvraag 7 === | === Examenvraag 7 === | ||
| Regel 120: | Regel 157: | ||
=== Examenvraag 8 === | === Examenvraag 8 === | ||
gegeven een 2-dimensionaal lineair stelsel Ax = b met<br> | gegeven een 2-dimensionaal lineair stelsel Ax = b met<br> | ||
A = [ ( | A = [ (<math>\alpha</math>+1) 1 ] | ||
[ | [ <math>\alpha</math> 1 ] | ||
We gebruiken de methode van Jacobi om een nulpunt te vinden. Bepaal alle waarden van alfa waarvoor de methode van Jacobi convergeert ( voor alle startwaarden ). | We gebruiken de methode van Jacobi om een nulpunt te vinden. Bepaal alle waarden van alfa waarvoor de methode van Jacobi convergeert ( voor alle startwaarden ). | ||
=== Examenvraag 9 === | |||
''Dubbel met examenvraag 6 (of toch ongeveer)''<br> | |||
* eem p(x) = a0 + a_1 x + ... + a_n x^n n is onbekend. p(0)=4, p(1)=9, p(2)=15, p(3)=18. De gedeelde differenties van orde 4 zijn allemaal gelijk aan 1. Bepaal a_3. | |||
=== Examenvraag 10 === | |||
Gegeven nog een hoop maple-uitvoer. Het gaat over een vijfdegraadsveelterm met een nulpunt in -0.31. Er wordt Newton-Raphson gebruikt om dat nulpunt te berekenen, en je krijgt een logaritmische plot van de fout. De plot is een heel normale, typische plot voor kwadratische convergentie. | |||
De vraag is: verklaar deze grafiek ( van de fout dus ). Wat is de convergentie-snelheid ?\" Als bijvraag kreeg ik \"het aantal juiste beduidende cijfers verdubbelt bij elke stap, hoe zie je dat in de grafiek ?. | |||
- | === Examenvraag 11 === | ||
Gegeven: A,b en twee berekende x matrices: Ax=b. De resultaten liggen ver uit elkaar. Bespreek stabiliteit van de methodes als machinenauwkeurigheid 10^-15 is. | |||
=== Examenvraag 12 === | |||
*Vraag: Veelterm <math>p(x)</math> met <math>p(-1)=p(0)=p(1)</math> en <math>p'(0)=1</math>. Geef alle veeltermen van zo laag mogelijke graad die hieraan voldoen. (Antwoord: p(0)+x-x³) | |||
=== Examenvraag 13 === | |||
Methode van het midden: bespreek grafiek, slecht geconditioneerd? | |||
=== Examenvraag 14 === | |||
Newton-Raphson + vereenvoudigde: bespreek een hele hoop grafieken en geef convergentiefactor en orde. | |||
=== Examenvraag 15 === | |||
Een Mapleprogramma voert onderstaande instructies uit, leg in detail uit waarom het programma besluit dat <math>y</math> niet gelijk is aan <math>0.3</math>.<br> | |||
x = 0.1 | |||
y = 3*0.1 | |||
if y == 0.3 | |||
then print "y is gelijk aan 0.3" | |||
else print "y is niet gelijk aan 0.3" | |||
Als uitvoer krijgen we:<br> | |||
x = 1.0000000000e-1 | |||
y = 3.0000000000e-1 | |||
y is niet gelijk aan 0.3 | |||
=== Examenvraag 16 === | |||
Stel de hermite interpolerende veelterm van graad 3 door <math>x_0</math> (<math>f_0\,</math> en <math>f'_0\,</math>) en <math>x_1</math> (<math>f_1\,</math>, <math>f'_1\,</math>) | |||
en | === Examenvraag 17 === | ||
Gegeven de methode van Newton Raphson. Verklaar de relatieve fouten grafiek van een willekeurige 5de graads veelterm met 3 nulpunten en geef de convergentiesnelheid (hint: die is 0 ) | |||
=== Examenvraag 18 === | |||
<math>A = \begin{pmatrix} | |||
7 & 2 & 10 \\ | |||
-1 & 4 & -5 \\ | |||
-1 & -1 & 0 | |||
\end{pmatrix} | |||
</math> | |||
De methode van de machten (met scalering) voor beginvector <math>[1,0,0]^T</math>. Benadering voor eigenvector bij eigenwaarde 5 geeft <math>x_1 = \ldots</math> (was gegeven). Benadering van eigenvector bij eigenwaarde 5 met startvector <math>[0,1,0]</math> geeft <math>x_2 = \ldots</math>. De vector <math>x_1</math> is geen veelvoud van <math>x_2</math>. Verklaar in detail hoe dit kan. (hint: normalisatie beïnvloedt alleen het niet-overlopen, en NIET de componenten van je <math>x_0</math> tov de andere eigenvectoren) | |||
=== Examenvraag 19 === | |||
''Dubbel met examenvraag 5''<br> | |||
(x-2)(x-4)...(x-30)<br> | |||
en dan diezelfde uitgewerkt.<br> | |||
De fouten verklaren die optreden bij de uitgewerkte veelterm.<br> | |||
=== Examenvraag 20 === | |||
niet-lineaire stelsels, grafieken bespreken. | |||
=== Examenvraag 21 === | |||
''Dubbel met examenvraag 2''<br> | |||
QR factorisatie, Q, R, Q'b, etc gegeven, stond helemaal in de cursus | |||
=== Examenvraag 22 === | |||
''Dubbel met examenvraag 5''<br> | |||
Neem de examenvragenbundel mee, want daar staat de vraag helemaal in uitgewerkt (in het ding da ni in TeX is uitgewerkt). Je hebt een Wilkinsonachtige veelterm. | |||
(x-2)(x-47)...(x-18) of zo iets. Als ge die zo in matlab uitvoert, dan is da ne juiste grafiek. als ge die echter eerst laat uitrekenen, dan geeft die fouten. De fouten worden heel groot als x groter wordt. Hoe komt dat? Je moet zeker een uitwerking geven van fouten enzo. Het komt er dan op neer dat de fout drastisch groter zal worden als x groter wordt. | |||
=== Examenvraag 23 === | |||
Je hebt de methode van NR om een stelsel van twee niet-lineaire vgln op te lossen. Deze gaat even naar een vreemde waarde op de grafiek. Dit is omdat de startvector dicht bij een waarde ligt waar de jacobiaan singulier is (det J = 0) . Gevraagd is de convergentieorde -en factor gevraagd. | |||
Dan heb je dezelfde vgln (ook grafiekjes) van de totale stapmethode en enkelv. stapmeth. Ook is convergentieorde en -factor gevraagd. Je kan die een beetje afleiden uit het grafiekje van de rel. fout. (let op: bij de laatste was da lineair, maar 't was een randgeval of zo iets) | |||
De twee grafieken raken, dus zijn het allemaal randgevallen die ge moet geven als oplossing. | |||
Bij enkelv. stapmeth.: waarom convergeert da naar het andere punt? -> singulier gedoe van J. Hoe kunnen we dat naar het andere punt laten gaan?-> andere volgorde van vgl oplossen. | |||
Een prulvraag waar het vooral op de mondelinge verdediging aankomt. | |||
=== Examenvraag 24 === | |||
Je krijgt een willekeurige 8*10-matrix (A), de Q en R ervan. Ook heb je een willekeurige 8*1-vector b. Dan geven ze je Q'b=bt .<br> | |||
Gevraagd: <math>\min_{x}||Ax-b||_2</math> tot op twee cijfers na de komma.<br> | |||
Een methode hoe je dit moet berekenen. | |||
=== Examenvraag 25 === | |||
Gegeven is een functie f(x) = sin(x) in het interval (-pi,pi).<br> | |||
Gevraagd : geef een bovengrens op de interpolatie-fout als ge weet dat uw interpolerende veelterm p is die in n-1 interpolatiepunten interpoleert. | |||
=== Examenvraag 26 === | |||
Gaat over Newton-Raphson en het bepalen van sqrt(a). Ge krijgt een iteratie-functie gegeven. Gevraagd : de functie bepalen die als wortel sqrt(a) heeft. En dan wa analyseren. | |||
de | === Examenvraag 27 === | ||
Gegeven een matrix en een startwaarde, bespreek dan wat er gebeurt als ge de methode van de machten toepast daarop. | |||
=== Examenvraag 28 === | |||
Examenvraag uit eerste oefenzitting | |||
=== Examenvraag 29 === | |||
Zij A een matrix waarbij alle elementen nul zijn behalve de elementen op de diagonaal en antidiagonaal. Schrijf een algoritme om het stelsel AX=B op te lossen. | |||
=== Examenvraag 30 === | |||
Stelsel van 2 niet-lineaire vergelijkingen wordt opgelost met Newton-Raphson. Convergentiegetal en -orde bepalen. (Je krijgt een grafiek van de relatieve fout en een plot van de nullijnen van de twee functies en de iteratiepunten) | |||
Voor welke start- en tussenwaarden moet de methode stopgezet worden? | |||
-- | === Examenvraag 31 === | ||
Matrix [ a b; c d] met | |||
a = 10^5 | |||
b = 10^5 | |||
c = (ad - 2) / b | |||
d = 3 - a | |||
Startwaarde [1; 1] | |||
We passen de methode der machten toe om de grootste eigenwaarde te vinden. Zoek convergentiegetal en orde. De gezochte eigenwaarde wordt maar met een beperkte nauwkeurigheid gevonden. Verklaar hoe dit komt. | |||
=== Examenvraag 32 === | |||
matrix met op eerste rij a1, a2,..., an en dan op de diagonaal onder de hoofddiagonaal allemaal eentjes en rest van elementen zijn 0. <br> | |||
Gegeven is dat λ<sub>1</sub> > dan alle andere eigenwaardes. <br> | |||
Dan is het volgende proggrammake gegeven;<br> | |||
Kies X^(0) willekeurig | |||
for i = 1 tot n | |||
X^(i) = A * X^(i-1) | |||
Scaleer deze zodat laatste component 1 wordt | |||
Nu moet je bewijzen dat de voorlaatste component naar λ<sub>1</sub> convergeert | |||
=== Examenvraag 33 === | |||
<math>\sqrt{1+x^3} - \sqrt{1+x^2}</math> evalueren in <math>x=10^{-5}</math> en formule uitrekenen zoals ze hierboven gegeven is.<br>Doe foutenanalyse en geef gedetailleerd antwoord. Kan je de waarde berekenen met 7 juiste beduidende cijfers? | |||
=== Examenvraag 34 === | |||
Gauss eliminatie - stelsels van lineaire vergelijkingen | |||
Is het mogelijk een analoog algoritme te maken met orthagonale transformaties? (zie hoofdst 13 sectie 13 in boek) | |||
Stel eerst een methode op om de hoek phi te bepalen zodat voor gegeven vector x | |||
> x:= linalg[matrix] (2, 1, [<math>x_1, x_2</math>]); | |||
x:= [<math>x_1, x_2</math>] | |||
de transformatie T (Givens rotatie) | |||
> T:= linalg[matrix]( 2, 2, [cos(phi), -sin(phi), sin(phi), cos(phi)] ); | |||
T:= [[Afbeelding:Linalg mat nw.gif]] | |||
als resultaat oplevert. | |||
> T*x= linalg[matrix]( 2, 1, [alpha, 0] ); | |||
Tx= [<math>\alpha</math> , 0] | |||
Ga ook na dat transformatie T orthogonaal is, dwz T vermenigvuldigd met zijn transpose is de eenheidsmatrix.<br> | |||
Is het orthogonaal zijn van T belangrijk voor de stabiliteit van een algoritme dat deze transformatie gebruikt om uitgaande van een niet-nul vector met 2 elementen een vector te maken waarvan het tweede element nul is?<br> | |||
Stel nu een algoritme op gebaseerd op de givens rotatie T analoog aan de eliminaatie methode van Gauss om een lineair stelsel van vergelijkingen op te lossen.<br> | |||
Wat is de hoeveelheid rekenwerk om de factorisatie op te bouwen?<br> | |||
Hoe ziet deze factorisatie eruit?<br> | |||
Hoe bereken je de uiteindelijke oplossing uitgaande van het getransformeerde stelsel? Hoeveel rekenwerk vraagt dit? | |||
=== Examenvraag 35 === | |||
Deze vraag wordt vanaf nu niet meer gesteld! Ik laat ze erop staan voor de liefhebbers. | |||
Beschouw volgend kleinste kwadraten probleem:<br> | |||
geg. een matrix A (met m rijen, n kolommen, m > n)<br> | |||
geg. vector b (met m componenten)<br> | |||
Gevraagd een vector x zodat | |||
||Ax-b||<small>2</small> minimaal is | |||
Gevraagd: Opl v stelsels lineaire vergelijkingen<br> | |||
Geeft het conditiegetal de conditie van de relatieve fouten weer?<br> | |||
Bespreek conditie van kleinste kwadratenprobleem<br> | |||
Hoe kan je conditie van dit probleem karakteriseren?<br> | |||
Ja mag aannemen dat matrix A van volle rang is. | |||
=== Examenvraag 36 === | |||
10/06/2013 | |||
Vraag 1: | |||
Beschouw de functie <math>f(x)=x^2+2x+c</math> met c kleiner of gelijk aan 1. Bespreek de conditie van het bepalen van de nulpunten in functie van c. | |||
Antwoord: Bereken <math>|f'(x)|</math>. Hoe groter dit getal is hoe slechter geconditioneerd. Slechtst geconditioneerd voor c ongeveer 1. | |||
===Examenvraag 37 === | |||
Bepaal a, b en c zodanig dat | |||
<math>f'_n=\frac{af_n+bf_{n+1}+cf_{n+2}}{h}+O(h^k)</math> | |||
Waarbij <math> f'_n = f'(x_n)</math> , en <math>f_j =f(x_j)</math> . De punten zijn equidistant. | |||
Antwoord: Stel een interpolerende lagrange veelterm op die door <math> f_{n} f_{n+1} </math> en <math> f_{n+2} </math> gaat.(Let op dat je je niet verwart met de n. Dit is niet het aantal interpolerende punten.) Bereken de lagrange termen voor 3 equidistante punten uit. Schrijf de veelterm dan op in functie van u en een error. Leid af naar u ( dit brengt een <math>\frac{1}{h} </math> buiten. Vul in voor u=o. | |||
= Examens = | |||
== Examen 19 januari 2006 == | |||
1) we hebben de functie f(x):exp(x^2)-1-x^2. Is deze numeriek stabiel? Bereken f(10^(-4)) met 10 beduidende juiste cijfers. | |||
2) bewijs via de interpolatie van Lagrange dat voor -h<x<h geldt: | |||
f'(x)= (hier stond een vgl met f(0) en f(h) f(-h) , kortom gewoon de afgeleide van de Langrange veelterm die je berekent rond de punten -h,0 en h) +D(n)(x) | |||
en geef de laatste term exact. | |||
Mijn bijvraag:Waar is die D het grootst? | |||
3) we hebben een functie F(x)=ax(1-x) en kiezen a=1/2. We zoeken de vaste punten van F, afh van a. Dan staat er een programmaatje gegeven in matlab en ne grafiek en de startwaarde is 2.01 en ge ziet da ge bij de eerste stap superdicht zit bij een vast punt, maar toch divergeert da. De vraag: leg grafiek uit en voor welke startwaarden krijgen we convergentie? | |||
Mijn bijvragen: hoe is de convergentie: lineair of superliniear of...? En wat is de convergentiefactor? | |||
4) dat gaat over die factorisatie met singuliere waarden. Ze geven u al de nodige matrices (dus die met de singuliere waarden, V,U,b,Ub,...). De vraag is: | |||
geef min over x van de 2-norm van Ax-b tot op 2 beduidende cijfers en leg dan uit hoe je de x zou berekenen waarvoor dit min bereikt wordt (keigoe te doen met u slides daarover behalve dan dat er een fout in de slides staat, yi=bi/sigmai moet vervangen worden door yi=bi'/sigmai) | |||
en | == Examen 26 januari 2007 (wiskunde) == | ||
# Gegeven de formule <math>\sqrt{1+x^3} - \sqrt{1+x^2}</math>. Bespreek de stabiliteit van deze formule voor <math>x = 10^{-5}</math>. Geef een gedetailleerd antwoord op basis van foutenanalyse. Kan je de waarde voor <math>x = 10^{-5}</math> met zeven beduidende cijfers bepalen? | |||
# Beschouw de substitutieformule <math>x^{(k+1)} = \exp(ax^{(k)})</math> met a reëel. Voor welke waarden van a zijn er één/geen/meerdere vaste punten? Als er een vast punt is, wanneer convergeert de methode dan? Naar welk punt? Voor welke startwaarden? Ken je hiervoor een geschikt stopcriterium? | |||
#* Bijvraag: voor welke a is er kwadratische convergentie? | |||
# Een hele hoop Maple-code over het oplossen van een lineair stelsel van twee vergelijkingen in twee onbekenden, met de methode van Newton-Raphson en die van Jacobi. | |||
#* Waarom geeft de methode van Newton-Raphson al na een stap de juiste oplossing, op afrondingsfouten na? (bijvraag: is dit in het algemeen ook zo, maw: wordt de oplossing van een lineair stelsel met de methode van Newton-Raphson steeds na 1 iteratiestap gegeven?) | |||
#* Bepaal de convergentiefactor en -orde van de methode van Jacobi. | |||
#* Waarom convergeert de methode van Jacobi zo traag? (bijvraag: kan je dit grafisch ook verklaren?) | |||
# Bespreek de conditie van de kleinste-kwadratenmethode. Je mag hierbij aannemen dat A van volle rang is. | |||
== Examen 29 januari 2007 == | |||
# veelterm van de vorm (x-2)(x-4)...(x-30). Waarom wordt de fout groter naar gelang een groter nulpunt wordt gekozen.(merk wel op dat naar gelang x->30 dat de fout weer kleiner wordt aangezien ai daar 1 is. Gewoon uitwerken naar f(x) = y(x) + E(x) en dan E(x) afzonderen. Dit geeft |emach| SOM(i=0 ..15) |ai| x^i. | |||
# Zij p(X) een veelterm van onbekende graad zodanig dat p(0) = 4, p(1) = 9, p(2) = 15 en p(3) = 18. Veronderstel dat alle gedeelde differenties van orde 4 gelijk zijn aan 1. Bepaal de coëfficiënt van x^3. | |||
# niet-lineaire vergelijkingen. Je krijgt een stelsel van twee vergelijkingen en de jacobiaan ervan. Bespreek het rare verloop(oorzaak is de singulariteit van de jacobiaan met die startwaarden, dus wanneer de determinant van de jacobiaan gelijk is aan 0, met de berekening van deze determinant kan je bepalen welke startwaarden hier aan voldoen). Verder moet je ook de convergentiefactor en orde geven van de NR methode en de vereenvoudigde NR methodes. | |||
# Je krijgt een matrix A, b en de QR vorm van A. Bereken minx ||Ax - B||. Welke methode gebruik je hiervoor? (kleinste kwadratenbenadering(slides) natuurlijk.) | |||
== Examen 8 juni 2007 == | |||
examenvragen die de industrieel ingenieurs die het overgangsprogramma naar burgie volgen kregen (voor zover 'k het me nog herinner): | |||
# Gegeven : | |||
een fuctie f(x) van de 6de graad | |||
x = 1.1 is een nulpunt | |||
een hoop matlab-code die ik niet verstond (alle matlab-oefenzittingen gebrost :-s) | |||
uit de commentaar was duidelijk dat ze Newton-Raphson toepasten | |||
een grafiek waarin duidelijk is dat de fout telkens kleiner wordt tot ongeveer 40 iteratiestappen, en daarna terug omhoog schiet, en terug zacht naar beneden gaat (en zo herhaalt zich dat). (grafiek zag er zo uit \|\|\|\| ) | |||
Gevraagd: | |||
leg in detail deze grafiek uit | |||
kun je een betere methode bedenken? | |||
oplossing : als ge de afgeleide van de gegeven functie berekent, dan is deze voor het opgegeven nulpunt ook nul, net zoals de derde en vierde afgeleide. We hebben dus te maken met een nulpunt met multipliciteit. => gevolg: newton-raphson = 1 - 0/0 | |||
Alternatief => Whittaker | |||
de | # Gegeven: | ||
Veelterm van nen bepaalde graad (5de graad?) | |||
De exacte integraal van deze veelterm van -1 tot 1 is een bepaalde waarde (waarde is gegeven) | |||
We gaan de integraal bepalen met twee kwadratuurformules. | |||
Weer matlabcode (:-s) | |||
x1 = -alfa, x2 = 0, x3 = alfa | |||
H1, H2 en H3 gegeven | |||
Eerste kwadratuurformule: | |||
alfa heeft bepaalde waarde | |||
de waarde van de kwadratuurformule is exact de opgegeven waarde | |||
Tweede kwadratuurformule: | |||
ander alfa waarde, de rest hetzelfde. | |||
de waarde van de kwadratuurfomule geeft nu een andere oplossing dan hierboven | |||
*( | Gevraagd: | ||
Stel dan volgende | - kunnen we hieruit besluiten dat de nauwkeurigheidsgraad van de eerste kwadratuurformule beter is dan de tweede? (uiteraard niet... anders zou hij't zo niet vragen :-p) | ||
- bereken de nauwkeurigheidsgraad van de kwadratuurforumules | |||
Oplossing: nauwkeurigheidsgraag van eerste was 2 en van tweede 5 (zie oefenzitting 8, opgave 3. en 4., in combinatie met p142 (en daarrond) in handboek) | |||
# Gegeven: | |||
f(x) = x² - x + 1 | |||
Weeral matlabcode (:-s) | |||
x* = 1 | |||
Door middel van substitutiemethodes word deze functie benaderd, ne keer langs links, en langs rechts (ik dacht voor x=0,9 en x=1,1) | |||
Twee grafieken gegeven, op de ene (x=0,9) zie je fout kleiner worden, op andere zie je fout groter worden. Verklaar. | |||
Zie dus figuur 2.10 op pagina 221. | |||
Bijvraag was iets van convergentiefactor bepalen ofzo | |||
# Gevraagd : wat gebeurd er als we "von Mises" op een matrix A uitvoeren met en een startvector X | |||
A = [ 2 1 -1 | 0 3 -5 | 0 0 -2 ] en X = [ -1 | 1 | 1 ] | |||
antwoord: normaal vinden we met von Mises (= Methode der machten) de grootste eigenwaarde. Nu niet, en dat komt omdat onze startwaarde toevallig een lineaire combinatie is van de twee andere eigenvectoren. | |||
== Examen 20 augustus 2007 == | |||
VRAAG 1: Examenvraag 15 | |||
VRAAG 2: Examenvraag 9 | |||
VRAAG 3: Beschouw de substitutieformule <math>x^{(k+1)} = \exp(ax^{(k)})</math> met a reëel. Voor welke waarden van <math>a</math> zijn er één/geen/meerdere vaste punten? Als er een vast punt is, wanneer convergeert de methode dan? Naar welk punt? Voor welke startwaarden? Ken je hiervoor een geschikt stopcriterium? | |||
VRAAG 4: Wat maple code over de methode der machten. Een driehoekige matrix is gegeven, met zijn eigenwaarden 2, 3 en -2. De methode Verder is ook een startvector gegeven. De methode lijkt te convergeren naar 2, maar convergeert tenslotte toch naar 3, dit zie je in een grafiek. Vraag: leg de grafiek uit. (Dit is omdat de startvector kan geschreven worden als een lineaire combinatie van de eigenvectoren van de matrix, en de component van de eigenvector bij 3 is zeer klein.) (Vraag uit een oude examenbundel) | |||
== Examen 14 januari 2008 (informatica) == | |||
#Examenvraag 5 | |||
#Examenvraag 2 (minimale ||r|| bepalen en zeggen hoe je de vector x die daarbij hoort kunt vinden) | |||
#Examenvraag 6 | |||
#Maple-sheet met stelsel van 2 niet-lineaire vergelijkingen en bijbehorende Jacobiaan gegeven. Grafieken van gewone newton-raphson en vereenvoudigde NR (enkelvoudige en totale stap methodes) -> Convergentieorde en -snelheid geven van beide methodes. | |||
== Examen 14 januari 2008 (1) == | |||
Exact hetzelfde examen als op 19 januari 2006. | |||
== Examen 14 januari 2008 (2) == | |||
Hetzelfde examen als 29 januari 2007. | |||
== Examen 18 januari 2008, voormiddag (informatica) == | |||
#Examenvraag 11 | |||
#Examenvraag 12 | |||
#Gegeven de methode van Newton Raphson. Verklaar de relatieve fouten grafiek van een willekeurige 5de graads veelterm met 3 nulpunten. | |||
#Examenvraag 32 | |||
== Examen 18 augustus 2008, voormiddag (informatica)== | |||
Zelfde als [[#Examen 20 augustus 2007|het herexamen van 20 augustus 2007]]. | |||
== Examen 8 juni 2009, namiddag == | |||
# Examenvraag 4 | |||
# Examenvraag 5 | |||
# Examenvraag 23 | |||
# Examenvraag 24 | |||
== Examen 9/06/09 voormiddag == | |||
#VRAAG 1: zelfde als examenvraag 1 van examen 20 augustus 2007 | |||
antwoord: 0.1 wordt binair door een repeterend patroon ofzo voorgesteld en dus als we inlezen wordt er een deel van dat patroon afgebroken en dus een kleine fout gemaakt. een geheel getal zoals 3 kan wel exact worden voorgesteld, en dus wordt de formule met fouten: | |||
fl(x) = 0.1(1+e) | |||
y= 3*x(1+e')(1+e) | |||
fl(y) = y(1+e'') | |||
en dus wordt er drie keer een foutje gemaakt en zal y dus niet meer exact gelijk aan 0.3 zijn (dat trouwens ook niet exact kan worden voorgesteld maar ook, zoals x, wordt afgebroken) | |||
bij het uitschrijven van y, wordt de binaire info terug omgezet naar decimaal talstelsel en vermits de fout die wordt gemaakt kleiner is als de machineprecisie zie je die eerst niet. | |||
#VRAAG 2: bereken een derde graad hermite interpolerende veelterm y0011(x) in twee interpolatie punten x0 en x1 met hun afgeleiden. (dus 1 graad hoger als het voorbeeld in boek deel II hoofdstuk 2 sectie 11) | |||
#VRAAG 3: 5de graadsveelterm gegeven en grafiek gegeven en maple printouts van van alles en ook de grafiek van de relatieve fout gegeven met verschillende punten en hun functie waarden uit die laatste grafiek.Gebruikte methode is Newton Rhapson. | |||
gevraagd: bespreek het verloop van deze foutenkromme in detail. Wat is de convergentiesnelheid? | |||
het was kwadratisch verloop, ma hij vroeg nog:" Kunt ge da eigelijk zien in de grafiek dat het kwadratisch is? Het kan toch ook superlineair zijn?" | |||
#VRAAG 4: zelfde als examenvraag 4. | |||
Antwoord: ge berekend dus eerst de eigenvectoren bij de eigenwaarden en dan ziet ge dat de startvector praktisch gelijk is aan een lineaire combinatie van twee eigenvectoren (-2 en 2) en daardoor zit uw iteratie in het begin vast in het vlak van die 2 eigenvectoren. Door de lichte afwijking op de vector (de .00001) komt de vector na genoeg iteraties toch uit het vlak en gaan we naar 3 itereren. Moest de startvector exact een lineaire combinatie van 2 eigen vectoren zijn dan zou men nooit naar 3 convergeren. (zie ook oefenzitting 10, Matlab sessie, daar hebben we ongeveer hetzelfde gedaan) | |||
De grafiek van de norm van de gevonden vector is ook gegeven en daar ziet ge dat hij eerst nen tijd op 2 staat en dan pas na 20 stappen begint te schommelen en toch naar 3 gaat. Waarom? Omdat hij pas de afwijking van de ideale waarden (de .00001) gaat zien nadat de iteratieve methode de juiste precisie heeft bereikt. Dat wil zeggen na 20 stappen (1 stap is 1 bit en 3 bits per getal nauwkeurig => 20 stappen voor 6 getallen nauwkeurig) | |||
== Examen 15/06/09 voormiddag == | |||
* 1) Gegeven: R = AX-B, norm van R, A en B alsook het conditiegetal van A en de diagonaal van L of U van een lu decompositie van A. | |||
**Gevraagd was of X een goede benadering was voor het exacte resultaat | |||
**De determinant van A | |||
**nog 2 kleine vraagjes | |||
* 2) Als we bij voorwaartse differenties een fout aanbrengen op f(k) ter grootte van E. | |||
** Hoe plant de fout zich voort, met welk patroon | |||
** Als we veronderstellen dat de differenties bij hoge graad zeer klein worden kunnen we op het einde van de tabel de grootte van de fout en de plaats van de fout aflezen, verklaar en leg uit. | |||
* 3) Beschouw de substititutiemethode x_(k+1) = exp(x_k). | |||
** Is er convergentie ? | |||
** Voor welke startwaarden ? | |||
** Nog een vraag waar ik niet kan opkomen | |||
* 4) Gegeven hoop maplecode over Newton-Raphson | |||
** Gevraagd wat de convergentiefactor en orde van convergentie | |||
** De laatste grafiek toonde een lineair gedrag. Verklaar waarom de methode traag convergeert. | |||
==Examen 15/06/2009 namiddag== | |||
'''Vraag 1''' | |||
Beschouw de volgende functie | |||
<math> f(x) = e^{x^2} - 1 - x^2</math> | |||
We willen de waarde berekenen van deze functie van x in de buurt van 0. We gebruiken daarvoor het volgend algoritme: | |||
a ↠<math>x^2</math> | |||
b ↠<math>e^a</math> | |||
f ↠b-1-a | |||
Is dit algoritme stabiel? | |||
Geef de waarde van <math>f(10^{-4})</math> met 10 juist beduidende cijfers. | |||
'''Vraag 2''' | |||
Gebruik de Lagrange formule om te bewijzen dat voor -h≤x≤h | |||
<math> f'(x)= \frac{1}{h^2}[\frac{2x-h}{2}f(-h)-2xf(0)+\frac{2x+h}{2}f(h)]+D(x) </math> | |||
met D(x) de differentiefout. Geef een uitdrukking voor D(x). | |||
'''Vraag 3''' | |||
Maple prints | |||
a) Verklaar waarom de methode van Newton Raphson in 1 iteratiestap op afrondingsfouten na de exacte oplossing vindt! | |||
b) Wat is de orde van de convergentie en wat is de convergentiefactor? | |||
c) Verklaar in detail waarom de totale stap vereenvoudigde Newton Raphson zo traag convergeert. | |||
'''Vraag 4''' | |||
Matlab output | |||
We hebben een random matrix A en een random rechterlid b. De singuliere-waarden-ontbinding van A berekend <math>A=USV^T</math> en de vector bt wordt berekend als <math>bt=U^Tb</math> | |||
Geef de waarde van <math>\min_{x}\|Ax-b\|_2</math> | |||
tot op 2 juiste beduidende cijfers. | |||
Geef aan welke methode je zal gebruiken om de vector te berekenen die de hierboven aangegeven 2-norm minimaal maakt. | |||
== Examen 16/06/09 namiddag == | |||
* 1) Bespreek de conditie van de nulpunten van x^2+2x+c (c<1). | |||
** Mondelinge Bijvraag: is de conditie goed/slecht voor de abolute of relatieve fout? | |||
* 2) Bewijs dat voor voorwaartse differentie geld dat DELTA(f_k/g_k) = [g_k*DELTA(f_k)-f_k*DELTA(g_k)] / (g_k*g_(k+1)) | |||
* 3) Beschouw de substititutiemethode x_(k+1) = exp(a*x_k). Voor welke a bestaan er geen/1/meerdere vast punten. Convergeert de methode? Zo ja, naar welke vaste punten? Voor welke startwaarden? Geef een goed stopcriterium. | |||
** Mondelinge Bijvraag: Convergentiesnelheid? | |||
* 4) Newton-Rhapson bij niet-lineair stelsel | |||
== Examen 19 juni 2009 == | |||
Vergelijk met examen 8 juni 2007. | |||
# Gegeven is de functie f(x) = (x - 1,1)^5 (maar uitgewerkt, dus f(x) = x^5 - 5,5*x^4 + ..., en er stond niet bij dat dit gelijk was aan (x-1,1)^5). Er is een Maplecode gegeven waarmee we via Newton-Raphson het nulpunt 1,1 willen bepalen. Men tekent de relatieve fouten en de grafiek daalt lineair, en schiet plots omhoog, daalt weer en terug omhoog, ... \|\|\|... Verklaar wat je ziet in de grafiek en geef een variant van Newton-Raphson waar dit probleem niet opduikt. | |||
# Beschouw <math>f(x) = \frac{a+x}{a-x}</math> waarbij a een parameter is. Definieer <math>\pi_n(x) = (x-x_0)(x-x_1)\ldots(x-x_n)</math>. Bewijs dat de interpolerende veelterm van f door 0 = x<sub>0</sub>, x<sub>1</sub>, ..., x<sub>n</sub> gegeven wordt door <math>y_n(x) = 1 + 2a\sum_{k=1}^n \frac{\pi_{k-1}(x)}{\pi_k(a)}</math>, en dat de interpolatiefout gelijk is aan <math>E_n(x) = \frac{2a\pi_n(x)}{(a-x)\pi_n(x)}</math>. | |||
# We gaan aan de hand van Maple het vast punt 1 van F(x) = x²-x+1 berekenen. We itereren telkens 1000 keer. De eerste keer beginnen we onder 1 (beginwaarde 0,9) en de tweede keer boven 1 (beginwaarde 1,1). De grafieken worden getekend en bij de eerste convergeert het monotoon naar 1 en bij de tweede divergeert het. Verklaar! | |||
# Wat gebeurt er als we de von Mises-methode toepassen op <math>\left[\begin{array}{ccc} 2 & 1 & -1 \\ 0 & 3 & -5 \\ 0 & 0 & -2\end{array}\right]</math> en beginvector <math>\left[\begin{array}{c} -1 \\ 1 \\ 1\end{array}\right]</math>? | |||
== Examen 7 juni 2010 == | |||
# Gegeven de volgende gegevens, kan je hiermee f(x1) uitrekenen? | |||
f[x0,x0,x1,x1] = 1; | |||
f´´(x0)=0; | |||
f´´(x1)=0; | |||
f´(x0)=0; | |||
f´(x1)=0; | |||
f(x0)=2; | |||
x0=0; | |||
x1=1; | |||
# Maple code: (beschrijving ervan: er werd van het getal 1000 50 keer de wortel genomen, daarna werd dit getal 50 keer gekwadrateerd. De vraag was dan: bespreek hoe het komt dat deze waarden zo verschillen. | |||
# Gegeven de iteratieformule x(k+1) = (x(k) - a)² - 1, met a > 0. Voor welke reële waarden van a en x(0) is er convergentie, en naar welke waarden van x gebeurt dit? Wanneer treedt er kwadratische convergentie op? | |||
# Gegeven maple code waar methode van de machten werd op toegepast. De gegevens werden erin genormeerd en mu werd uitgezet op de grafiek. Daarop was te zien hoe die convergeerde naar de dominante eigenwaarde. Ook werd er een grafiek gegeven die de relatieve fout van mu (in logaritmische schaal) uitzet tov het aantal iteratiestappen. Die was dalend en in 'rechte'-vorm. Je moest de grafieken bespreken en een bijvraag was hoe je op de laatste grafiek de convergentiesnelheid kon zien. | |||
== Examen 18 juni 2010 namiddag== | |||
#oefening uit de eerste oefenzitting | |||
#Zij A een matrix waarbij alle elementen nul zijn, behalve die op de diagonaal en die op de antidiagonaal. Schrijf een algoritme om het stelsel AX=B op te lossen, met B een gegeven vector. Bereken de hoeveelheid rekenwerk. | |||
#Maple code: niet-lineair stelsel, Newton-Raphson, Grafiek van de twee functies en de benaderingen van het snijpunt, grafiek van de relatieve fout tov aantal iteratiestappen. Hoe snel convergeert de metode? Verklaar in detail. Wat is de orde van convergentie en de convergentiefactor? Waarom convergeert de methode in dit geval zo snel/traag? Verklaar dit in detail. Bij welke startwaarden of tussenpunten stopt de methode? | |||
#A=<math>\left[\begin{array}{cc} a & c \\ d & b \end{array}\right]</math> met <math>a=10^5</math>, <math>c=10^5</math>, <math>b=3-a</math>, <math>d=\frac{ab-2}{c}</math>. Hierop voeren we de methode van de machten uit. Bepaal de orde van convergentie en de convergentiefactor. Bij de benadering van de dominante eigenwaarde bereiken we slechts een beperkte nauwkeurigheid (emach=<math>10^{-16}</math>). Verklaar dit in detail. | |||
== Examen 10 juni 2011 voormiddag== | |||
'''Exact''' hetzelfde als het examen van 19 januari 2006. | |||
== Examen 17 juni 2011 (Informatica) == | |||
1) 2x2-matrix A met zeer grote getallen (orde 10^40 enz) en matrix B. 2 benaderende oplossingen voor stelsel Ax = B gegeven, met verschillende methodes berekend (er is niet gegeven welke methodes). Vraag: zeg iets over de stabiliteit van de gebruikte methodes | |||
2) veelterm p(x) met p(-1) = p(0) = p(1) en p'(0) = 1. Geef alle veeltermen van zo laag mogelijke graad die hieraan voldoen. Antwoord: via methode der onbepaalde coëfficiënten: p(0)+x-x³ | |||
3) maple-output voor het zoeken van een nulpunt van een veelterm. De veelterm, zijn grafiek en zijn afgeleide zijn gegeven. de methode van newton-raphson wordt gebruikt. Op de grafiek zien we dat de relatieve fout lineair daalt. Vraag: waarom is de convergentie zo traag? wat zegt dit over het nulpunt? geef de convergentiefactor. waarom zijn slechts 7 van de cijfers van de benaderende oplossing juist, terwijl we over 16 cijfers beschikken? Bijvraag: kan je de convergentiefactor grafisch tonen op de grafiek? Antwoord: trage konvergentie want meervoudig nulpunt. Meervoudigheid was 3 dus konvergentiefactor 2/3. Slechte benadering want slecht geconditioneerd probleem. | |||
4) gegeven: A = compagnion-matrix (zie laatste schriftelijke oefenzitting), kies een willekeurige startvector X(0). for(i=1..n) { X(i) = A*X(i-1); scaleer X(i) zodat het laatste element van deze vector 1 wordt; }. Vraag: toon aan dat het voorlaatste element van de vector X(n) konvergeert naar de (strikt) grootste eigenwaarde. | |||
== Examen 24 juni 2011 namiddag == | |||
Hetzelfde examen als 8 juni 2007 met als enige verschil vraag 2: | |||
2) Gegeven enkele equidistante punten Xi, f(Xi). Er staat een fout epsilon op 1 van die punten, namelijk op Xk, f(Xk). Als je de tabel van voorwaartse (=gedeelde) differenties opstelt kan je zien hoe de fout zich propageert. Herken je een bepaald patroon? (duh, anders zou hij het niet vragen) Je mag er van uit gaan dat de differenties met hogere graad naar 0 gaan. Hoe kan je vinden op welk punt Xk de fout zat en hoe groot die is? | |||
oplossing: | |||
Stel gewoon een tabel op voor N elementen: | |||
X1 f(X1) | |||
... | |||
Xk-2 f(Xk-2) | |||
Xk-1 f(Xk-1) | |||
Xk f(Xk)+epsilon | |||
Xk+1 f(Xk+1) | |||
Xk+2 f(Xk+2) | |||
... | |||
Xn f(Xn) | |||
en reken die dan een paar stappen uit. Je zal zien dat de fout epsilon groter wordt en zich uitbreidt. Ook wisselt de fout steeds van teken: dit komt omdat als je de gedeelde differenties uitrekent, je soms -(f(Xk)+epsilon) moet doen, wat de epsilon negatief maakt. Als je vervolgens nog eens moet aftrekken, -(f(Xk)-epsilon) dus, dan wordt epsilon weer positief. Uiteindelijk bekom je volgend patroon in de fouten, dat eigenlijk de driehoek van pascal/binonium van newton is! | |||
eps | |||
eps | |||
eps -4*eps | |||
eps -3*eps | |||
eps -2*eps 6*eps | |||
-eps 3*eps | |||
eps -4*eps | |||
-eps | |||
eps | |||
enzoverder. De fout verbreedt dus, maar de tabel wordt kleiner. Uiteindelijk zal je dus met 1 getal overblijven (want de f(x)'en worden allemaal 0 als je blijft doorrekenen. Stel dat dat getal bijvoorbeeld -10*eps is. Je zoekt in de driehoek van pascal op waar die "10" staat, en zie je dat op de 6e rij staat tussen 1 5 10 12 10 5 1. De 10 staat op de 3e plaats links, maar ook op 3e plaats rechts. Dit komt overeen met k of n-k = 3, dus het punt waar de fout op zit staat op derde plaats in de tabel OF op de n-3 plaats. | |||
== Examen 11 juni 2012 voormiddag (Informatica) == | |||
Vraag 1: We hebben de volgende gegevens van de functie <math>f(x)</math>. | |||
*<math>f[x_0,x_0,x_1,x_1] = 1</math> | |||
*<math>f''(x_0) = 0</math> | |||
*<math>f''(x_1) = 0</math> | |||
*<math>f'(x_0) = 0</math> | |||
*<math>f'(x_1) = 0</math> | |||
*<math>f(x_0) = 2</math> | |||
*<math>x_0 = 0</math> | |||
*<math>x_1 = 1</math> | |||
Kunnen we met behulp van deze gegevens de waarde van de functie bepalen in <math>x_1</math>, d.w.z., <math>f(x_1)</math>? | |||
Oplossing: | |||
<math>f[x_0,x_0,x_1,x_1] = \frac{f[x_0,x_1,x_1] - f[x_0,x_0,x_1]}{x_1 - x_0} = \frac{\frac{f[x_1,x_1] - f[x_0,x_1]}{x_1 - x_0} - \frac{f[x_0,x_1] - f[x_0,x_0]}{x_1 - x_0}}{x_1 - x_0}</math> | |||
<math>f[x_0,x_1] = \frac{f(x_1) - f(x_0)}{x_1 - x_0} = \frac{f(x_1) - 2}{1 - 0} = f(x_1) - 2</math> | |||
<math>f[x_0,x_0,x_1,x_1] = \frac{\frac{0 - (f(x_1) - 2)}{1 - 0} - \frac{f(x_1) - 2 - 0}{1 - 0}}{1 - 0} = -f(x_1) + 2 - f(x_1) + 2 = -2f(x_1) + 4 = 1</math> | |||
<math>f(x_1) = \frac{3}{2}</math> | |||
Vraag 2: Er is maple code gegeven die er ongeveer zo uit ziet: | |||
*x = 1000 | |||
*for(1 to 50) | |||
**x = sqrt(x); | |||
*end | |||
*for(1 to 50) | |||
**x = x*x; | |||
*end | |||
*x | |||
De output is | |||
* x = 1000 | |||
* x = 1009 (Denk ik, toch iets in die buurt.) | |||
Verklaar in detail waarom deze waarden zo verschillen. | |||
Oplossing: | |||
Werk dit uit met de <math>fl(\dots)</math> notatie. | |||
Bijvraag: Zal er na de 50 worteltrekkingen ook al een relatief grootte fout te zien zijn? | |||
Vraag 3: Zij het iteratieproces <math>x^{k+1} = (x^k - a)^2 + 1</math> voor <math>a > 0</math> gegeven. Voor welke reële waarden van <math>a</math> en <math>x^{(0)}</math> is er convergentie naar een reële waarde <math>x</math>? Wanneer treedt er kwadratische convergentie op? | |||
Oplossing: | |||
<math>x^{k+1} = F(x^k)</math> met <math>F(x) = (x - a)^2 + 1</math> voor <math>a > 0</math> | |||
<math>x^* = F(x^*)</math> | |||
<math>x = (x - a)^2 + 1</math> | |||
<math>x^2 - 2ax - x + 1 + a^2 = 0</math> | |||
<math>x^*_{1,2} = \frac{2a + 1 \pm \sqrt{4a - 3}}{2}</math> | |||
<math>4a - 3 \geq 0</math> => <math>a \geq \frac{3}{4}</math> | |||
Er is convergentie als <math>|F\ '(x)| < 1</math> | |||
<math>F\ '(x) = 2(x -a)</math> dus <math>|F'(x^*_{1,2}) = 1 \pm \sqrt{4a - 3}| < 1</math> dus <math>a = \frac{3}{4}</math> | |||
Er is kwadratische convergentie als <math>\rho = 0</math> dus als <math>F\ '(x^*_{1,2}) = 1 - \sqrt{4a - 3} = 0</math> dus als <math>a = 1</math>. | |||
Vraag 4: Methode der machten | |||
<math>A = \left[\begin{array}{ccc} 9 & 1 & -1 \\ 0 & 10 & -5 \\ 0 & 0 & 8\end{array}\right]</math> en <math>x_0 = \left[\begin{array}{c} -1 \\ 1 \\ 1\end{array}\right]</math> | |||
Omdat de matrix A bovendriehoeks is, vinden we de eigenwaarden van A op de hoofddiagonaal: 9, 10, 8. De dominante eigenwaarde is dus 10. Er wordt maple code gegeven om die de methode der machten toepast met normalisatie. De methode wordt 100 keer uitgevoerd met k = 1..100. Er wordt een grafiek gegeven van elke benadering van <math>\lambda _1</math> (=10) voor elke iteratie. Er wordt ook zo'n grafiek gegeven voor de relatieve fout. | |||
Verklaar de grafieken die hierboven gegenereerd werden. Wat is de orde van convergentie en wat is de convergentiefactor? Wat zou er gebeuren als we in de methode hierboven geen normalisatie zouden gebruiken? Bijvraag: kan je de convergentiefactor ook afleiden uit de 2<math>^{de}</math> grafiek? | |||
Oplossing: | |||
De orde is lineair (dit is altijd zo bij de methode der machten) | |||
De convergentiefactor is <math>\frac{\lambda _2}{\lambda _1} = \frac{9}{10}</math> | |||
De methode der machten is enkel geldig als <math>\xi _1 \ne 0</math>. <math>\xi _1</math> halen we uit <math>x_0 = \xi _1E_1 + \xi _2E_2 + \xi _3E_3</math> en <math>E_i</math> vinden we door <math>(A - \lambda _iI)X = 0</math> | |||
<math>\lambda _1 = 10 \Rightarrow \left[\begin{array}{ccc} -1 & 1 & -1 \\ 0 & 0 & -5 \\ 0 & 0 & -2\end{array}\right]\left[\begin{array}{ccc} x_1 \\ x_2 \\ x_3\end{array}\right] = 0 \Rightarrow \begin{array}{c}x_1 = x_2 \\ x_2 = x_1 \\ x_3 = 0\end{array} \Rightarrow E_1 = \left[\begin{array}{ccc} 1 \\ 1 \\ 0\end{array}\right]</math> | |||
<math>\lambda _2 = 9 \Rightarrow \left[\begin{array}{ccc} 0 & 1 & -1 \\ 0 & 1 & -5 \\ 0 & 0 & -1\end{array}\right]\left[\begin{array}{ccc} x_1 \\ x_2 \\ x_3\end{array}\right] = 0 \Rightarrow \begin{array}{c}x_1 = x_1 \\ x_2 = 0 \\ x_3 = 0\end{array} \Rightarrow E_2 = \left[\begin{array}{ccc} 1 \\ 0 \\ 0\end{array}\right]</math> | |||
<math>\lambda _3 = 8 \Rightarrow \left[\begin{array}{ccc} 1 & 1 & -1 \\ 0 & 2 & -5 \\ 0 & 0 & 0\end{array}\right]\left[\begin{array}{ccc} x_1 \\ x_2 \\ x_3\end{array}\right] = 0 \Rightarrow \begin{array}{c}x_1 = -1.5x_3 \\ x_2 = 2.5x_3 \\ x_3 = x_3\end{array} \Rightarrow E_3 = \left[\begin{array}{ccc} -3 \\ 5 \\ 2\end{array}\right]</math> | |||
Uit <math>x_0 = \xi _1E_1 + \xi _2E_2 + \xi _3E_3</math> halen we dat <math>\xi _1 = \frac{-3}{2} \ne 0</math> Dus de methode der machten mag gebruikt worden met startvector <math>x_0</math> | |||
Als we geen normalisatie zouden gebruiken zouden we overflow krijgen. | |||
== Examen 22 juni 2012 voormiddag == | |||
Examenvraag 28 t/m 31 (hij vraagt ze zelfs op volgorde!) | |||
== Examen 10 juni 2013 (9u00) == | |||
# Bespreek de conditie van de nulpunten van <math> \displaystyle x^2 + 2x+c </math> met <math>c \leq 1</math>. Is de conditie goed/slecht voor de abolute of relatieve fout? | |||
# Gegeven <math> f'_n = \frac{a \cdot f_n+b \cdot f_{n+1}+c \cdot f_{n+2}}{h} + O(h^k) </math>. Bereken <math>a</math>, <math>b</math> en <math>c</math> zodat <math>k</math> maximaal is. | |||
# Beschouw de substititutiemethode <math> x^{(k+1)} = e^{ax^{(k)}} </math>. Voor welke a bestaan er geen/1/meerdere vast punten. Convergeert de methode? Zo ja, naar welke vaste punten? Voor welke startwaarden? Geef een goed stopcriterium. | |||
# Newton-Rhapson bij een niet-lineair stelsel vergelijkingen. | |||
== Examen 11 juni 2013 (14u00) == | |||
# Gegeven <math>\int^{a+h}_{a-h} f(x) = H_\frac{-2}{3} \cdot f(a-\frac{2h}{3}) + H_0 \cdot f(a) + H_\frac{2}{3} \cdot f(a+\frac{2h}{3})</math>. Bereken de waarden van de gewichten zodat de nauwkeurigheidsgraad maximaal is, hoeveel is deze nauwkeurigheidsgraad? | |||
# Gegeven <math> x^2 + dx - 2 </math>. Wanneer is het probleem van het zoeken van dit nulpunt goed geconditioneerd? Hoeveel gaan de nulpunten verschuiven bij een verschuiving van <math>d</math>? | |||
# Beschouw de substititutiemethode <math> x^{(k+1)} = -e^{-(ax^{(k)})^2} </math>. Treedt er convergentie op? Zoja, wat zijn de convergentiefactor, convergentiesnelheid en convergentie-orde? | |||
# Gegeven de matrix <math>A = \begin{pmatrix} | |||
22 & -7 \\ | |||
87 & 28 | |||
\end{pmatrix}</math>, <math>x = \begin{pmatrix} | |||
x_{1}\\ | |||
x_{2} | |||
\end{pmatrix}</math> en <math>b =\begin{pmatrix} | |||
1\\ | |||
4 | |||
\end{pmatrix}</math> We passen de methode van Jacobi toe op deze matrix. Bepaal de convergentiefactor en de convergentie-orde. Waarom is er een trage convergentie? Geef grafisch weer hoe er geconvergeerd wordt. | |||
== Examen 23 augustus 2013 (8u00) == | |||
'''Vraag 1:''' (Oefenzitting 2, Probleem 6), enige verschil staat '''vetgedrukt'''. | |||
We weten dat <math>\lim_{x\rightarrow \infty} (1 + 1/x)^x = e^1</math>. We gaan de waarde <math>e</math> benaderen door <math>\tilde{e}_k = (1 + 1/x_k)^{x_k}</math> uit te rekenen voor | |||
* <math>x_k = 2^k</math> and | |||
* <math>x_k = 2^k</math>. | |||
In de figuren hieronder geven we de relatieve fout weer, d.w.z. <math>| \frac{\tilde{e}_k-e}{e}|</math>. De eerste figuur geeft de relatieve fout voor de machten van 2 terwijl de tweede figuur de fouten voor machten van 10 weergeeft. | |||
(figuur) | |||
Waarom zijn de twee grafieken zo verschillend? '''Doe hiervoor voor beide gevallen een foutenonderzoek.''' | |||
Kan men hieruit afleiden met welke basis en met hoeveel beduidende cijfers de computer werkt? | |||
Verklaar in detail je antwoord. | |||
'''Vraag 2:''' | |||
Bepaal de Hermite interpolatie die de functiewaarden en de eerste afgeleiden in <math>x_0</math> en <math>x_1</math> interpoleert. (Geen waarden gegeven.) | |||
Bepaal de interpolatiefout. | |||
'''Vraag 3:''' (MATLAB) | |||
* Data: | |||
** Een veelterm van graad 5. | |||
** De afgeleide van de veelterm. | |||
* MATLAB: | |||
** Code voor Newton-Rhapson. | |||
* Figuren: | |||
** Grafiek van de veelterm. | |||
** Log-plot van de relatieve foutentermen. | |||
[[Bestand:Graph1-230813.png]] | |||
[[Bestand:Plot2-230813.png]] | |||
We zien dat deze veelterm nulpunten heeft in <math>x = -2</math>, <math>x = -4/3</math> en <math>x = 1</math>. We gebruiken Newton Rhapson met <math>x^{(0)}=2</math> en k = 100. | |||
Waarom convergeert deze zo traag? Kunnen we hier iets uit afleiden over het gezochte nulpunt? | |||
Kunnen we uit de foutenplot de convergentie factor afleiden? Kunnen we hier iets uit afleiden over het gezochte nulpunt? | |||
We werken in een machine met 16 beduidende cijfers. Waarom is de gevonden oplossing zo onnauwkeurig? | |||
'''Vraag 4:''' | |||
Matrix A (3x3, gegeven). | |||
We gebruiken de methode van de machten met startvector <math>X_1 = [1, 0, 0]</math>. Deze levert eigenvector <math>X_1^{'}</math> (gegeven) horende bij eigenwaarde <math>\lambda = 5</math>. | |||
Dit proces herhalen met startvector <math>X_2 = [0, 1, 0]</math> levert <math>X_2^{'}</math>, wederom met eigenwaarde <math>\lambda = 5</math>. <math>X_1^{'}</math> is nochtans geen veelvoud van <math>X_2^{'}</math>. | |||
Verklaar in detail. | |||
== Examen 10 juni 2016 (namiddag) == | |||
[[Media:ExamenNumerieke10-06-2016-nm.pdf | Examen 10 juni 2016 (NM)]] | |||
== Examen 15 juni 2016 (8u00) == | |||
# Men probeert e te benaderen via de formule (1 + 1/x)^x voor grote x. Men gebruikt als x'en zowel 2^k als 10^k. Gegeven grafieken voor de relatieve fout ten opzichte van k voor de twee methoden. Verklaar het verschil in de grafieken, wat is de basis van de machine waarop het uitgevoerd werd, hoeveel beduidende cijfers in die basis gebruikt ze? Mondeling vroeg hij wel waarom de relatieve fout bij de 10^k-methode minimaal 10^-8 wordt, ongeveer de helft van de beduidende decimale cijfers ondersteund door de machine. | |||
# Ontwerp een algoritme dat een lineair stelsel oplost waarbij de coëfficiëntenmatrix alleen niet-nul-elementen heeft op de diagonaal en antidiagonaal (linksonder naar rechtsboven). Hoeveel rekenwerk vraagt je algoritme? (Niet exact, Big-O notatie volstaat.) | |||
# Gegeven de functie f(x) = (1 - sin(x))/cos(x). De limiet van f(x) naar pi/2 is 0. Dit "nulpunt" (bestaat technisch gezien niet) wordt benaderd met de bisectiemethode, Maple-code gegeven. Je krijgt ook als Maple-output een grafiek van de relatieve fout ten opzichte van het aantal iteraties. | |||
## Kan je uit de grafiek de convergentiesnelheid (lineair, kwadratisch, superlineair, ...), convergentieorde en convergentiefactor afleiden? Komt dit overeen met de theorie? | |||
## Is dit probleem slecht geconditioneerd? | |||
## De relatieve fout blijft "vast hangen" rond 10^-9, terwijl de benadering uitgevoerd wordt met 20 beduidende decimale cijfers. Verklaar. | |||
# Gegeven de matrix A = [[7, 2, 10], [-1, 4, -5], [-1, -1, 0]]Men past de methode van de machten toe (met scalering) met als startvector [1, 0, 0]^T, en komt voor de eigenwaarde 5 de eigenvector X1 uit. Bij startvector [0, 1, 0]^T komt men voor dezelfde eigenwaarde de eigenvector X2 uit. X1 ~ [0.9733, -0.1622, -0.1622]^T en X2 ~ [0.5345, 0.8018, -0.2673]^T Deze vectoren zijn geen veelvoud van elkaar. Hoe kan dit? Verklaar met detail. Mondeling vroeg hij nog wat het concrete verband is tussen de uitkomstvector en de startvector. | |||
== Examen 15 juni 2017 (NM) == | |||
[[Media:Examen15juni2017.pdf | Examen 15 juni 2017 (NM)]] | |||
== Examen 16 juni 2017 (NM)== | |||
[[Media:NumWis_16_06_17.pdf | Examen 16 juni 2017 (NM)]] | |||
== Examen 19 juni 2017 (NM) == | |||
[[Media:Examen_numerieke_wiskunde_19_juni_2017.pdf | Examen 19 juni 2017 (NM)]] | |||
== Examen 18 augustus 2017 (VM) == | |||
[[Media:18_08_2017.pdf | Examen 18 augustus 2017 (VM)]] | |||
== Examen juni 2018 == | |||
[[Media:NW_19_06_18.pdf | Examen 19 juni 2018 (NM)]] | |||
[[Media:examen2706.pdf | Examen 25 juni 2018 (VM)]] | |||
[[Media:Examen_Numerieke_Wiskunde_27_juni.pdf | Examen 25 juni 2018 (NM)]] | |||
== Examen 11 Juni 2019 (08u) == | |||
Examen was uitzonderlijk niet mondeling. | |||
'''Vraag 1''' | |||
Drie vragen oplossen op max 1 pagina. | |||
'''a) Methode van de Machten voor Bovendriehoeksmatrix''' | |||
<math> | |||
A = \begin{bmatrix} | |||
5 & 4 & 3 \\ | |||
0 & -8 & \\ | |||
0 & 0 & 1 | |||
\end{bmatrix} | |||
</math> | |||
Naar welk getal convergeert de methode van de machten? | |||
'''b) Interpolatie''' | |||
<math> | |||
f(x) = \frac{1}{x} | |||
</math> | |||
Zal de fout op een willekeurig punt dalen als meer interpolatiepunten worden toegevoegd. | |||
'''c) Machinefout''' | |||
Kan <math>\epsilon_\text{mach} / 2</math> correct voorgesteld worden op een computer (IEEE standaard). | |||
'''Vraag 2: Numerieke integratie''' | |||
<math> | |||
\int^{1}_{0} f(x) = H_1 f(0) + H_2 f(0,5) + H_3 f(1) + H_4 f'(0,5) | |||
</math> | |||
Bepaal de coëfficiënten en nauwkeurigheidsgraad. Herken je de formule? | |||
'''Vraag 3: Conditie stelsel lineaire vergelijkingen''' | |||
<math> | |||
Ax = b , ||A|| = 2,3 | |||
</math> | |||
<math> | |||
||b|| = 2,14*10^{-4} | |||
</math> | |||
<math> | |||
\bar{b} = b + 1-^{-10} e_1 | |||
</math> | |||
Conditiegetal van a = 4*10^5 | |||
Maak een schatting van het verschil, is deze betrwoubaar. | |||
'''Vraag 4: Substitutiefuncties''' | |||
<math> | |||
f(x) = x^3 - \frac{24}{50} x^2 + \frac{21}{400} x + 1 | |||
</math> | |||
<math> | |||
F_1(x) = \frac{x^3 - \frac{24}{50} x^2+ 1}{ - \frac{21}{400}} | |||
</math> | |||
<math> | |||
F_2(x) = x - f(x)/f'(x) | |||
</math> | |||
<math> | |||
\bar{b} = b + 1-^{-10} e_1 | |||
</math> | |||
<math> | |||
x^*_1 = -0,02 | |||
</math> | |||
<math> | |||
x^*_{2,3}= 0,25 | |||
</math> | |||
Gegeven 2 tabellen die convergeren naar -0,02, welke hoort bij welke substitutiefunctie. Bepaal de convergentiefactor met behulp van de tabel (als dit zinnig is). | |||
Een andere tabel die start bij 0,2 en convergeert naar 0,25 met <math>F_2</math>. Bepaal de convergentiefactor en verklaar. | |||
== Examen 14 juni 2019 == | |||
[[Media:NW-2019-06-14-0800.pdf | Examen 14 juni 2019 8 uur]] | |||
== Examen 18 juni 2019 (8u) == | |||
'''Vraag 1''' | |||
'''Drie vragen oplossen op max 1 pagina.''' | |||
'''a)''' | |||
Stel dat de afgeleide van de functie <math>f(x)=x^{4}</math> in <math>x = 0,01</math> wordt benaderd door <math>df = \frac{f(x) - f(x-h)}{h}</math>. | |||
Kies je h best (a) gelijk of (b) groter of (c) kleiner dan <math>\sqrt{\epsilon_{mach}}</math>? Waarom? | |||
'''b)''' | |||
Stel we gebruiken de methode van Newton om het nulpunt <math>x^{*}</math> van een functie <math>f(x)</math> te berekenen met <math>|x^{(k)}-x^{*}| < TOL</math>. | |||
Teken <math>f(x)</math> in de omgeving van het nulpunt <math>x^{*}</math> waarvoor het stopcriterium <math>|f(x^{*})| < TOL</math> te optimistisch is (m.a.w. waar het te vroeg stopt.) | |||
'''c)''' | |||
< | <math> | ||
A = \begin{bmatrix} | |||
4 & -4 & 2 \\ | |||
0 & -7 & 7 \\ | |||
0 & 0 & 1 | |||
\end{bmatrix} | |||
</math> | |||
Naar welk getal convergeert de methode van de machten? Waarom is dat zo en hoe kom je hierop? | |||
'''Vraag 2''' Stel je moet een computerprogramma schrijven dat <math>sin(x)</math> benadert met minimaal 6 juiste cijfers. Enkel +, -, x en / mogen gebruikt worden. | |||
Leg gedetailleerd stap voor stap uit hoe je te werk gaat. Let op: de sinusfunctie mag wel uitgevoerd worden om het programma af te leiden, maar mag niet in het programma zelf gebruikt worden uiteraard. | |||
'''Vraag 3''' | |||
Gegeven een ijle matrix A waarvoor alleen <math>A_{i,i-2}, A_{i,i-1}, A_{i,i}, A_{i,i+1}, A_{i,i+2}</math> niet nul zijn. ''(in de rijen 1, 2 en N-1, N bestaan de elementen die erbuiten vallen natuurlijk gewoon niet --> zie 'bandmatrix')'' | |||
Stel dat je dit oplost met de methode van Gauss-Seidel en je in <math>\frac{n}{5}</math> iteraties de gevraagde nauwkeurigheid bereikt. Hoeveel rekenkundige bewerkingen (+, -, *, /) worden er uitgevoerd? | |||
Vergelijk dit aantal met LU-factorisatie waar er geen rekening wordt gehouden met het ijle karakter van de matrix. | |||
'''Vraag 4''' | |||
<math>x^{(k+1)} = x^{(k)}-\frac{f(x^{(k)})}{g^{(k)}}</math> | |||
met <math>g^{(k)} = \frac{f(x^{(k)}+f(x^{(k)}))-f(x^{(k)}}{f(x^{(k)})}</math> | |||
We gebruiken bovenstaande formule om de nulpunten van <math>f(x)</math> te berekenen. Je kan onder redelijke voorwaarden kwadratische convergentie verwachten. | |||
'''1)''' Bewijs dat dit geldt. | |||
'''2)''' Is er een voordeel t.o.v de methodes die we in de cursus hebben gezien? | |||
'''Antwoord op 20 lijnen''' | |||
== | == Examen 24 juni 2019 (8u) == | ||
[[Media:24_juni_2019_numerieke_examen.pdf | Examen 24 juni 2019 8 uur]] | |||
== Examen 24 juni 2019 (13u) == | |||
[[Media:ExamenvragenNumeriekeWiskunde2406201913.pdf | Examen 24 juni 2019 13 uur]] | |||
== Examen 03 september 2019 (8.30u) == | |||
[[Media:Numerieke_augustus_2019_(2).pdf | Examen 3 september 2019]] | |||
== Examen 11 juni 2020 (8u) == | |||
[[Media:Examen_Numerieke_Wiskunde_11_06_2020.pdf | Examen 11 juni 2020]] | |||
== Examen 12 juni 2020 (12u) == | |||
[[Media:Examen12juni2020.pdf | Examen 12 juni 2020 12u]] | |||
[[Media:Examen12juni2020Antwoorden.pdf | Examen 12 juni 2020 12u (Eigen uitgewerkte antwoorden)]] | |||
=== | == Examen 15 juni 2020 == | ||
[[Media:ExamNumWisk_150620.pdf | Examen 15 juni 2020 8u]] | |||
[[Media:Examen-15Juni2020-12u30.pdf | Examen 15 juni 2020 12u30]] | |||
=== | == Examen 22 juli 2020 == | ||
[[Media:Examen Numerieke Wiskunde 22 08 2020.pdf | Examen 22 augustus 2020 8u]] | |||
== Examen 17 juni 2021 == | |||
[[Media:ExamenNumerieke17Juni.pdf | Examen 17 juni 2021]] | |||
=== | == Examen 21 juni 2021 == | ||
'''Vraag 1''' | |||
'' | |||
(zelfde vraag als op het examen van 12 juni 2020) | |||
= | Gegeven dat <math>f(x) = \frac{e^x-1}{x} </math> | ||
a) Geef de conditie van <math>f(x)</math> (ook voor <math>|x| -> \infty</math>). | |||
(x | |||
b) Geef de stabiliteit van de oplossingsmethode (ook voor <math>|x| -> \infty</math>). | |||
'''Vraag 2''' | |||
(zelfde vraag als op het examen van 12 juni 2020) | |||
Bepaal de gewichten voor volgende kwadratuurformule zodat de nauwkeurigheidsgraad maximaal is: | |||
<math>\int^{a+h}_{a-h} f(x) = H_\frac{-3}{4} \cdot f(a-\frac{3h}{4}) + H_0 \cdot f(a) + H_\frac{3}{4} \cdot f(a+\frac{3h}{4})</math> | |||
Wat is deze nauwkeurigheidsgraad? | |||
'''Vraag 3''' | |||
Gegeven dat <math>F(x) = een veeltermfunctie die ik mij niet meer herinner</math>, | |||
a) Geef de vaste punten van <math>F(x)</math>. | |||
b) Convergeert dit? Indien dit het geval is, wat is dan de convergentiesnelheid? Indien deze lineair is, geef dan ook de convergentiefactor. Geef ook de orde van elk punt. (niet meer zeker van de exacte bewoording van de prof.) | |||
c) Voor welke startpunten convergeert dit? Leg uit en maak ook een grafiek waarop je voor verschillende karakteristieke punten schetst hoe ze convergeren. (ook hier niet zeker hoe het er exact stond, maar de essentie is hopelijk wel duidelijk) | |||
=== | = Schakelprogramma Master (Toegepaste) Informatica = | ||
== Examen 10 juni voormiddag/17 augustus voormiddag == | |||
'''Vraag 1''' | |||
We lossen met een bepaalde methode het stelsel AX=B op. We krijgen de berekende vector Y als benadering voor X. Hieronder volgt een gedeelte van de bijbehorende Matlab-sessie: | |||
>> R=A*Y-B; | |||
>> norm(R) | |||
ans = 4.4409e-15 | |||
>> norm(A) | |||
ans = 1.4281e+01 | |||
>> norm(B) | |||
ans = 4.3197e+01 | |||
>> cond(A) | |||
ans = 4.0892e+11 | |||
>> [L,U] = lu(A); | |||
>> diag(U)' | |||
ans = | |||
Columns 1 through 5 | |||
1.2618e+00 1.0839e+00 1.5534e+00 1.9028e-10 -8.1081e+01 | |||
Columns 6 through 10 | |||
1.8780e+00 1.7355e+00 1.5833e+00 -9.5583e-01 -1.7088e-01 | |||
*Hoe nauwkeurig is de berekende oplossing Y?<!-- Kan je niet weten: X-Y geeft dit (absolute fout), maar X is niet gekend! + analyse conditie--> | |||
*Is de berekende oplossing Y van het probleem een exacte oplossing van een nabijgelegen probleem?<!-- Ja. Ay=B+R (residus) --> | |||
*Kan je de determinant van A berekenen?<br />Zo ja, geef dan een benaderende waarde.<!-- determinant: product van de diagonaalelementen. det(U) = 1.407e-9; +-det A = det(U) =/= 0, dus A is inverteerbaar en regulier --> | |||
*Kan je <math>||A^{-1}||</math> berekenen?<!-- Ja, want inverteerbaar. Stelling 3.3 p56, p67, p73 + analyse conditie. Kleine (relatieve) residus kan toc nog afkomstig zijn van grote (relatieve) fouten op X als de conditie van de matrix A slecht is. K(A) is van orde grootte 10^11. In de berekeningen zullen 11 beduidende cijfers verloren gaan.--> | |||
'' | '''Vraag 2''' | ||
Bepaal de gewichten in de kwadratuurformule | |||
<math>\int^{1}_{0}f(x)dx\approx H_{0}f_{0} + H_{1}f_{1} + H_{0}^\prime f_{0}^\prime + H_{1}^\prime f_{1}^\prime</math> | |||
zodanig dat de naukeurigheidsgraad zo hoog mogelijk is. | |||
<math>f_{i}=f(i),\quad i=0,1;</math> | |||
<math>f_{i}^\prime='(i),\quad i=0,1;</math> | |||
waarbij f' een notatie is voor de afgeleide van f. | |||
'''Vraag 3''' | |||
Beschouw de substitutieformule | |||
- | <math>x^{(k+1)}=-exp(x^{(k)})</math>. | ||
Ga na of er convergentie is. | |||
Voor welke startwaarden? | |||
Ken je een goed stopcriterium hiervoor? | |||
'''Vraag 4''' | |||
Zoals examenvraag 3: http://people.cs.kuleuven.be/~marc.vanbarel/NumWis/Illus/Zeros2/STELSELS1.html, maar dan met de volgende gegevens: | |||
u = x² + (y-2)²-3.7 | |||
v = x² + y² - 4 | |||
(matrix J is 2x 2y-4; 2x 2y) | |||
*a) Verklaar waarom de tweede en volgende iteraties bij Newton-Raphson op een horizontale lijn gelegen zijn.<!--singuliere Jacobiaan--> | |||
*b) Voor welke startpunten (en tussenliggende punten) werkt de methode van Newton-Raphson niet. | |||
*c) Wat is de orde van convergentie en wat is de convergentiefactor? | |||
*d) Wat is de orde van convergentie en wat is de convergentiefactor? | |||
*e) Verklaar in detail waarom de totale stap vereenvoudigde Newton-Raphson zo traag convergeert. | |||
== Examen 30 juni 2022 == | |||
-- | '''Vraag 1''' | ||
Beschouw de functie f(x) = (x²-1)-(x+1) | |||
Matlab functie: (x.x-1)-(x+1) | |||
Vraag a) Bespreek de conditie van het probleem ten opzichte van de relatieve fout voor een | |||
willekeurige waarde van x | |||
Vraag b) Bespreek de numerieke stabiliteit van de berekeningsmethode voor een willekeurige | |||
waarde van x | |||
'''Vraag 2''' | |||
gegeven: | |||
x1 - x0 = 1 | |||
f(x0) = 1 | |||
f(x1) = 2 | |||
f'(x0) = -1 | |||
f[x0, x0, x1, x1] = 4 | |||
zoek f'(x1) | |||
'''Vraag 3''' | |||
Beschouw de functie f(x) = x³ - 4x² + 4x | |||
waarvan we de nulpunten gaan benaderen met de methode van Newton-Raphson. | |||
Vraag a) Bepaal de bijhorende functie F(x). | |||
Vraag b) Zijn er vaste punten? Zo ja, bereken elk van deze vaste punten. | |||
Vraag c) Ga voor elk vast punt na of er lokale convergentie is naar dit vast punt? Zo ja, wat is de | |||
convergentiesnelheid (lineair, superlineair, kwadratisch, . . . )? Als de convergentiesnelheid linear | |||
is, geef dan ook een numerieke waarde voor de convergentiefactor. Komt dit ook overeen met wat | |||
je theoretisch weet over de convergentiesnelheid van de methode van Newton-Raphson? | |||
Vraag d) Voor welke startwaarden is er convergentie, voor welke startwaarden is er divergentie? | |||
Staaf je antwoord op deze vraag op een grafische manier door voor verschillende karakteristieke | |||
gevallen van de startwaarde een schets te maken van het iteratieproces. | |||
== voorbeeldexamen == | |||
[[Media:Voorbeeldexamen-numerieke.pdf]] - Oplossingen vind je onder: https://drive.google.com/open?id=1-B0Yyv4DDNyFGW6-vjMv-jtfVWmB9-7_ | |||
= Mogelijk nuttige documenten = | |||
[[Media:Splines_en_Differenties.pdf]]: Een aantal stellingen en inzichten ivm. B-Splines en gedeelde differenties. Geloven op eigen risico. | |||
[[Categorie:1bw]] | |||
[[Categorie:2bi]] | |||
[[Categorie:Aoi]] | |||
Huidige versie van 30 jun 2022 17:51

Didactisch Team
| Academiejaar | Professor(en) | Assistent(en) |
|---|---|---|
| 2019-2020 | Professor1, Professor2 | Assistent1, Assistent2 |
| 2020-2021 | Professor1, Professor2 | Assistent1, Assistent2 |
Samenvattingen
Klik hier om de samenvattingen te bekijken
Korte samenvatting + enkele oplossingen Dries 2018-2019: google drive map
Het examen
2021-2021: Examen van prof. Van Barel. Door corona duurde het examen 3 uur en bestond het examen uit 3 vragen. Het bericht van de prof op Toledo onder '2018-2019' geldt ook dit jaar. De vragen kwamen bijna exact overeen met vragen 1, 5 en 6 van het voorbeeldexamen onderaan de pagina.
Vraag 1: Gegeven een bepaalde functie, bespreek de conditie en de stabiliteit. Vraag 2: Gegeven een kwadratuurformule, bepaal de gewichten zodat de nauwkeurigheidsgraad zo hoog mogelijk ligt. Wat is de nauwkeurigheidsgraad? Vraag 3: Gegeven een matrix en een grafiek (semilogy) van de relatieve fout met respect tot het aantal uitgevoerde stappen. Verklaar de grafiek (redelijke vage vraag). Bereken convergentieorde en convergentiefactor. Bepaal orde en factor grafisch. Komt dit overeen met je antwoord uit vraag b?
2018-2019: Het examen was uitzonderlijk schriftelijk omdat Marc Van Barel wegens medische redenen een groot deel van het semester afwezig was. Het examen was dan ook als een schriftelijk examen opgesteld, waardoor de vragen misschien niet erg representatief zijn voor de vragen mét mondelinge toelichting. Wel is het nog steeds open boek, al is het niet meer 'all you can carry' zoals het voorheen was (zie bericht toledo onderaan). Het examen bestond uit een opgavebundel, waarna je de vragen (sommigen met een lengte/regel-restrictie) op blanco papier moest oplossen. Het examen duurde in totaal 4 uur.
Bericht van de prof op Toledo: Het examen is open-boek in de volgende betekenis: Het handboek, de tekst ivm splines en de slides alsook een afdruk van de illustraties (o.a. jupyter notebooks) mogen op het examen gebruikt worden waarbij er hier en daar iets mag bijgeschreven worden ter verduidelijking. Opgaven van oefeningen en oplossingen mogen NIET gebruikt worden.
Vakevaluatie
Elk puntje hieronder is iemands mening. Verander aub geen puntjes. Als je een andere mening hebt, gelieve ze onderaan toe te voegen.
Kwaliteit cursus (prijs, duidelijkheid, overeenkomst met les, ...)
- 2017: Handgeschreven "slides" en een handboek. Uiteindelijk moet je enkel de essentie kennen, en die staat in de slides.
Studiebelasting (aantal studiepunten in verhouding met bestede tijd)
- 2017: Zeventien oefenzittingen. Zeventien. Er is ook een practicum waarvoor je meer dan een semester de tijd krijgt. Als je het werk kunt spreiden, is dat zeker te doen. Tijdens de blok is het niet meer werk dan andere vakken van 6 sp.
- 2022: Practicum kregen we dit jaar een dikke maand voor, dit is voldoende als je er genoeg aan werkt tijdens de paasvakantie anders kan het wel wat krapper worden.
Plaats binnen de opleiding (nodige voorkennis, overlap met andere vakken, relevantie van het vak,...)
- 2017: Volgens de informatici is het meer een wiskundevak. Volgens de wiskundigen is het meer een informaticavak. Zorg dat je BVP, lineaire algebra en calculus/wiskunde I eerst gevolgd hebt.
- 2021: Dit vak is eerder een ingenieursvak en is niet heel nuttig voor wiskundigen. Voor informatici kan het wel nuttig zijn aangezien dit een mogelijk onderzoeksdomein is in de master computerwetenschappen.
Manier van lesgeven bij hoorcolleges (snelheid, verstaanbaarheid, structuur, nut, ...)
- 2017: De meesten zijn niet wild van de uitleg van Marc Van Barel.
- 2019: De uitleg van Marc Van Barel is nog steeds niet geweldig, maar de assistent die overpakte vanaf les 3 of 4 was pakken beter.
- 2022: De uitleg is nog altijd niet beter.
Evaluatie oefenzittingen/labo's (nut, begeleiding, ...)
- 2017: De oefenzittingen zijn niet echt noodzakelijk.
- 2022: De oefenzittingen zijn nuttig (als je een goede assistent hebt) als je niet echt mee bent met de uitleg van de prof.
Examen (mate waarin het een weerspiegeling is van de cursus, examenvorm, ...)
- 2017: Je moet eigenlijk alleen de essentie begrijpen. Dat zeggen de assistenten ook herhaaldelijk. Je mag alles meenemen wat je wilt, dus sommigen profiteren hiervan door dit beestaf te drukken.
- 2018: Het examen is niet langer open-boek zoals vorig jaar. Bericht van de prof op Toledo: Het examen is open-boek in de volgende betekenis: Het handboek, de tekst ivm splines en de slides alsook een afdruk van de illustraties (o.a. jupyter notebooks) mogen op het examen gebruikt worden waarbij er hier en daar iets mag bijgeschreven worden ter verduidelijking. Opgaven van oefeningen en oplossingen mogen NIET gebruikt worden.
Extra oefenmateriaal
Deze oefeningen zijn afkomstig van de website van de burgerlijk ingenieurs.
http://examens.wina.be/images/Oefeningen_Burgies.doc
Verder is hier een oud document dat ik nog terugvond. Het bevat opmerkingen en hulp bij de toenmalige oefenzittingen. (kan zijn dat die ondertussen wat veranderd zijn) De opmaak is verre van geslaagd, de EPS plots zitten er niet meer in, en het delta symbool is een lege verzameling symbool geworden. Voor wie het toch nog wil kan het wel een hulp zijn: Media:OefenzittingenNW.pdf.
Losse examenvragen
Git met oplossingen: https://github.com/KULeuven-CS/Numerieke-Wiskunde
Hieronder een aantal examenvragen die van een aantal bronnen zijn samengeraapt...
Deze kunnen onduidelijk, onvolledig, onmogelijk,... zijn...
De opmaak is niet altijd helemaal in orde
Hulp met wiskundesyntax vindt je hier: http://meta.wikimedia.org/wiki/Help:Formula
Geachte heer Van Barel heeft de neiging om deze vragen letterlijk opnieuw te vragen, zie maar dat ge deze kent dus! Maar wie de rest niet leert is nog dommer dan Jos Ghysen, en 't is niet omdat hij een tv programma gehad heeft dat gij dat ook zult hebben! Leren dus!. Oppassen voor bijvragen (if any). Maar in het jaar 2007 was dat toch niet meer waar, van die vragen opnieuw gesteld te hebben, dus zeker gewoon helemaal leren Geldt nog steeds in het jaar 2007 hoor, je moet gewoon wat geluk hebben. En in 2008 was het weer zo dus maak alles wat hieronder staat maar!
Examenvraag 1
Gegeven een programma
som = 0.0 for i = 0.0:0.1:1.0 verschil = i - som % == 0 som = som + 0.1
end
Output:
verschil = 0 verschil = 0 .. verschil = 1.1.. e-15
(Syntaxverduidelijking: % en alles wat erachter komt is commentaar, geen modulo ofzo.)
Verklaar waarom het verschil plots niet meer gelijk is aan 0. Waarvoor staat dat getal?
Examenvraag 2
Je krijgt de QR ontbinding van een matrix A, en Q'.b.
gevraagd: ||r|| en hoe zou je x bepalen dat hoort bij die ||r||.
Examenvraag 3
Je krijgt een paar grafiekjes en maple code over Newton Raphson en de vereenvoudigde Newton Raphson (niet lineaire stelsels). Je krijgt een viertal kleine "verklaar waarom" vraagjes.
Examenvraag 4
Maple afdruk: laatste vraag van de examenvragen in de winabundel (Die over het bepalen van eigenwaarden met de methode van de machten).
Uit de matrix A = [2 1 -1; 0 3 -5; 0 0 -2] wordt de dominante eigenwaarde berekend. De startwaarden zijn: [-1.00001 1.00002 1]. Op de grafiek is zichtbaar dat er eerst naar 2 lijkt te convergeren, maar uiteindelijk toch de juiste eigenwaarde 3 gekozen wordt. Het berekenen gebeurt met de methode van de machten met normalisatie.
- Hoe komt het dat er eerst naar 2 geconvergeerd wordt?
- Waarom uiteindelijk toch naar 3?
- Wat als er geen normalisatie gebruikt zou worden?
Examenvraag 5
Maple printout
p_2 is p_1 uitgewerkt (geëxpandeerd): [met b_i gegeven constanten, elke bi heeft een mantisse met precisie 10]
die twee geplot.
een keer van interval x=2..6
een keer van interval x=6..20
een keer van interval x=20..30
(de fout in het derde interval was veel groter dan in het eerste interval)
#Maple code om te testen Digits := 10; f:= product((x-2.0*i),i=1..15); g:=collect(f,x); plot([f,g],x=2..6); plot([f,g],x=6..20); plot([f,g],x=20..30);
De vraag is hoe het komt dat de fouten groter zijn voor grotere nulpunten. Als bijvraag moest ik verklaren waarom de fout voor vb. x=28 van de orde 10^13 is en van welke orde de fout dan is voor x = 4. ( dat laatste zag je niet op de grafiek, omdat de fout heel klein was tegenover de grootte van de functie zelf ).
Examenvraag 6
Er is een functie van de vorm
p(x) = a0 + a1x + a2x^2 + ... +an*x^n (n is niet gekend)
p(0) = 5
p(1) = 9
p(2) = 15
p(3) = 18
Gegeven dat alle gedeelde differenties van de vierde graad 1 zijn.
Geef a3.
Examenvraag 7
Maple printout
Newton Raphson.
gegeven: f(x), df(x)
plot van de fout voor a=-1 (naar nulpunt -0.3....)
geef de convergentiesnelheid in detail.
Examenvraag 8
gegeven een 2-dimensionaal lineair stelsel Ax = b met
A = [ (+1) 1 ]
[ 1 ]
We gebruiken de methode van Jacobi om een nulpunt te vinden. Bepaal alle waarden van alfa waarvoor de methode van Jacobi convergeert ( voor alle startwaarden ).
Examenvraag 9
Dubbel met examenvraag 6 (of toch ongeveer)
- eem p(x) = a0 + a_1 x + ... + a_n x^n n is onbekend. p(0)=4, p(1)=9, p(2)=15, p(3)=18. De gedeelde differenties van orde 4 zijn allemaal gelijk aan 1. Bepaal a_3.
Examenvraag 10
Gegeven nog een hoop maple-uitvoer. Het gaat over een vijfdegraadsveelterm met een nulpunt in -0.31. Er wordt Newton-Raphson gebruikt om dat nulpunt te berekenen, en je krijgt een logaritmische plot van de fout. De plot is een heel normale, typische plot voor kwadratische convergentie.
De vraag is: verklaar deze grafiek ( van de fout dus ). Wat is de convergentie-snelheid ?\" Als bijvraag kreeg ik \"het aantal juiste beduidende cijfers verdubbelt bij elke stap, hoe zie je dat in de grafiek ?.
Examenvraag 11
Gegeven: A,b en twee berekende x matrices: Ax=b. De resultaten liggen ver uit elkaar. Bespreek stabiliteit van de methodes als machinenauwkeurigheid 10^-15 is.
Examenvraag 12
- Vraag: Veelterm met en . Geef alle veeltermen van zo laag mogelijke graad die hieraan voldoen. (Antwoord: p(0)+x-x³)
Examenvraag 13
Methode van het midden: bespreek grafiek, slecht geconditioneerd?
Examenvraag 14
Newton-Raphson + vereenvoudigde: bespreek een hele hoop grafieken en geef convergentiefactor en orde.
Examenvraag 15
Een Mapleprogramma voert onderstaande instructies uit, leg in detail uit waarom het programma besluit dat niet gelijk is aan .
x = 0.1 y = 3*0.1 if y == 0.3 then print "y is gelijk aan 0.3" else print "y is niet gelijk aan 0.3"
Als uitvoer krijgen we:
x = 1.0000000000e-1 y = 3.0000000000e-1 y is niet gelijk aan 0.3
Examenvraag 16
Stel de hermite interpolerende veelterm van graad 3 door ( en ) en (, )
Examenvraag 17
Gegeven de methode van Newton Raphson. Verklaar de relatieve fouten grafiek van een willekeurige 5de graads veelterm met 3 nulpunten en geef de convergentiesnelheid (hint: die is 0 )
Examenvraag 18
De methode van de machten (met scalering) voor beginvector . Benadering voor eigenvector bij eigenwaarde 5 geeft (was gegeven). Benadering van eigenvector bij eigenwaarde 5 met startvector geeft . De vector is geen veelvoud van . Verklaar in detail hoe dit kan. (hint: normalisatie beïnvloedt alleen het niet-overlopen, en NIET de componenten van je tov de andere eigenvectoren)
Examenvraag 19
Dubbel met examenvraag 5
(x-2)(x-4)...(x-30)
en dan diezelfde uitgewerkt.
De fouten verklaren die optreden bij de uitgewerkte veelterm.
Examenvraag 20
niet-lineaire stelsels, grafieken bespreken.
Examenvraag 21
Dubbel met examenvraag 2
QR factorisatie, Q, R, Q'b, etc gegeven, stond helemaal in de cursus
Examenvraag 22
Dubbel met examenvraag 5
Neem de examenvragenbundel mee, want daar staat de vraag helemaal in uitgewerkt (in het ding da ni in TeX is uitgewerkt). Je hebt een Wilkinsonachtige veelterm.
(x-2)(x-47)...(x-18) of zo iets. Als ge die zo in matlab uitvoert, dan is da ne juiste grafiek. als ge die echter eerst laat uitrekenen, dan geeft die fouten. De fouten worden heel groot als x groter wordt. Hoe komt dat? Je moet zeker een uitwerking geven van fouten enzo. Het komt er dan op neer dat de fout drastisch groter zal worden als x groter wordt.
Examenvraag 23
Je hebt de methode van NR om een stelsel van twee niet-lineaire vgln op te lossen. Deze gaat even naar een vreemde waarde op de grafiek. Dit is omdat de startvector dicht bij een waarde ligt waar de jacobiaan singulier is (det J = 0) . Gevraagd is de convergentieorde -en factor gevraagd. Dan heb je dezelfde vgln (ook grafiekjes) van de totale stapmethode en enkelv. stapmeth. Ook is convergentieorde en -factor gevraagd. Je kan die een beetje afleiden uit het grafiekje van de rel. fout. (let op: bij de laatste was da lineair, maar 't was een randgeval of zo iets) De twee grafieken raken, dus zijn het allemaal randgevallen die ge moet geven als oplossing. Bij enkelv. stapmeth.: waarom convergeert da naar het andere punt? -> singulier gedoe van J. Hoe kunnen we dat naar het andere punt laten gaan?-> andere volgorde van vgl oplossen. Een prulvraag waar het vooral op de mondelinge verdediging aankomt.
Examenvraag 24
Je krijgt een willekeurige 8*10-matrix (A), de Q en R ervan. Ook heb je een willekeurige 8*1-vector b. Dan geven ze je Q'b=bt .
Gevraagd: tot op twee cijfers na de komma.
Een methode hoe je dit moet berekenen.
Examenvraag 25
Gegeven is een functie f(x) = sin(x) in het interval (-pi,pi).
Gevraagd : geef een bovengrens op de interpolatie-fout als ge weet dat uw interpolerende veelterm p is die in n-1 interpolatiepunten interpoleert.
Examenvraag 26
Gaat over Newton-Raphson en het bepalen van sqrt(a). Ge krijgt een iteratie-functie gegeven. Gevraagd : de functie bepalen die als wortel sqrt(a) heeft. En dan wa analyseren.
Examenvraag 27
Gegeven een matrix en een startwaarde, bespreek dan wat er gebeurt als ge de methode van de machten toepast daarop.
Examenvraag 28
Examenvraag uit eerste oefenzitting
Examenvraag 29
Zij A een matrix waarbij alle elementen nul zijn behalve de elementen op de diagonaal en antidiagonaal. Schrijf een algoritme om het stelsel AX=B op te lossen.
Examenvraag 30
Stelsel van 2 niet-lineaire vergelijkingen wordt opgelost met Newton-Raphson. Convergentiegetal en -orde bepalen. (Je krijgt een grafiek van de relatieve fout en een plot van de nullijnen van de twee functies en de iteratiepunten) Voor welke start- en tussenwaarden moet de methode stopgezet worden?
Examenvraag 31
Matrix [ a b; c d] met a = 10^5 b = 10^5 c = (ad - 2) / b d = 3 - a
Startwaarde [1; 1]
We passen de methode der machten toe om de grootste eigenwaarde te vinden. Zoek convergentiegetal en orde. De gezochte eigenwaarde wordt maar met een beperkte nauwkeurigheid gevonden. Verklaar hoe dit komt.
Examenvraag 32
matrix met op eerste rij a1, a2,..., an en dan op de diagonaal onder de hoofddiagonaal allemaal eentjes en rest van elementen zijn 0.
Gegeven is dat λ1 > dan alle andere eigenwaardes.
Dan is het volgende proggrammake gegeven;
Kies X^(0) willekeurig for i = 1 tot n X^(i) = A * X^(i-1)
Scaleer deze zodat laatste component 1 wordt
Nu moet je bewijzen dat de voorlaatste component naar λ1 convergeert
Examenvraag 33
evalueren in en formule uitrekenen zoals ze hierboven gegeven is.
Doe foutenanalyse en geef gedetailleerd antwoord. Kan je de waarde berekenen met 7 juiste beduidende cijfers?
Examenvraag 34
Gauss eliminatie - stelsels van lineaire vergelijkingen
Is het mogelijk een analoog algoritme te maken met orthagonale transformaties? (zie hoofdst 13 sectie 13 in boek)
Stel eerst een methode op om de hoek phi te bepalen zodat voor gegeven vector x
> x:= linalg[matrix] (2, 1, []); x:= []
de transformatie T (Givens rotatie)
> T:= linalg[matrix]( 2, 2, [cos(phi), -sin(phi), sin(phi), cos(phi)] );
T:= 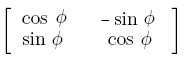
als resultaat oplevert.
> T*x= linalg[matrix]( 2, 1, [alpha, 0] ); Tx= [ , 0]
Ga ook na dat transformatie T orthogonaal is, dwz T vermenigvuldigd met zijn transpose is de eenheidsmatrix.
Is het orthogonaal zijn van T belangrijk voor de stabiliteit van een algoritme dat deze transformatie gebruikt om uitgaande van een niet-nul vector met 2 elementen een vector te maken waarvan het tweede element nul is?
Stel nu een algoritme op gebaseerd op de givens rotatie T analoog aan de eliminaatie methode van Gauss om een lineair stelsel van vergelijkingen op te lossen.
Wat is de hoeveelheid rekenwerk om de factorisatie op te bouwen?
Hoe ziet deze factorisatie eruit?
Hoe bereken je de uiteindelijke oplossing uitgaande van het getransformeerde stelsel? Hoeveel rekenwerk vraagt dit?
Examenvraag 35
Deze vraag wordt vanaf nu niet meer gesteld! Ik laat ze erop staan voor de liefhebbers.
Beschouw volgend kleinste kwadraten probleem:
geg. een matrix A (met m rijen, n kolommen, m > n)
geg. vector b (met m componenten)
Gevraagd een vector x zodat
||Ax-b||2 minimaal is
Gevraagd: Opl v stelsels lineaire vergelijkingen
Geeft het conditiegetal de conditie van de relatieve fouten weer?
Bespreek conditie van kleinste kwadratenprobleem
Hoe kan je conditie van dit probleem karakteriseren?
Ja mag aannemen dat matrix A van volle rang is.
Examenvraag 36
10/06/2013 Vraag 1: Beschouw de functie met c kleiner of gelijk aan 1. Bespreek de conditie van het bepalen van de nulpunten in functie van c.
Antwoord: Bereken . Hoe groter dit getal is hoe slechter geconditioneerd. Slechtst geconditioneerd voor c ongeveer 1.
Examenvraag 37
Bepaal a, b en c zodanig dat
Waarbij , en . De punten zijn equidistant.
Antwoord: Stel een interpolerende lagrange veelterm op die door en gaat.(Let op dat je je niet verwart met de n. Dit is niet het aantal interpolerende punten.) Bereken de lagrange termen voor 3 equidistante punten uit. Schrijf de veelterm dan op in functie van u en een error. Leid af naar u ( dit brengt een buiten. Vul in voor u=o.
Examens
Examen 19 januari 2006
1) we hebben de functie f(x):exp(x^2)-1-x^2. Is deze numeriek stabiel? Bereken f(10^(-4)) met 10 beduidende juiste cijfers.
2) bewijs via de interpolatie van Lagrange dat voor -h<x<h geldt: f'(x)= (hier stond een vgl met f(0) en f(h) f(-h) , kortom gewoon de afgeleide van de Langrange veelterm die je berekent rond de punten -h,0 en h) +D(n)(x) en geef de laatste term exact. Mijn bijvraag:Waar is die D het grootst?
3) we hebben een functie F(x)=ax(1-x) en kiezen a=1/2. We zoeken de vaste punten van F, afh van a. Dan staat er een programmaatje gegeven in matlab en ne grafiek en de startwaarde is 2.01 en ge ziet da ge bij de eerste stap superdicht zit bij een vast punt, maar toch divergeert da. De vraag: leg grafiek uit en voor welke startwaarden krijgen we convergentie? Mijn bijvragen: hoe is de convergentie: lineair of superliniear of...? En wat is de convergentiefactor?
4) dat gaat over die factorisatie met singuliere waarden. Ze geven u al de nodige matrices (dus die met de singuliere waarden, V,U,b,Ub,...). De vraag is: geef min over x van de 2-norm van Ax-b tot op 2 beduidende cijfers en leg dan uit hoe je de x zou berekenen waarvoor dit min bereikt wordt (keigoe te doen met u slides daarover behalve dan dat er een fout in de slides staat, yi=bi/sigmai moet vervangen worden door yi=bi'/sigmai)
Examen 26 januari 2007 (wiskunde)
- Gegeven de formule . Bespreek de stabiliteit van deze formule voor . Geef een gedetailleerd antwoord op basis van foutenanalyse. Kan je de waarde voor met zeven beduidende cijfers bepalen?
- Beschouw de substitutieformule met a reëel. Voor welke waarden van a zijn er één/geen/meerdere vaste punten? Als er een vast punt is, wanneer convergeert de methode dan? Naar welk punt? Voor welke startwaarden? Ken je hiervoor een geschikt stopcriterium?
- Bijvraag: voor welke a is er kwadratische convergentie?
- Een hele hoop Maple-code over het oplossen van een lineair stelsel van twee vergelijkingen in twee onbekenden, met de methode van Newton-Raphson en die van Jacobi.
- Waarom geeft de methode van Newton-Raphson al na een stap de juiste oplossing, op afrondingsfouten na? (bijvraag: is dit in het algemeen ook zo, maw: wordt de oplossing van een lineair stelsel met de methode van Newton-Raphson steeds na 1 iteratiestap gegeven?)
- Bepaal de convergentiefactor en -orde van de methode van Jacobi.
- Waarom convergeert de methode van Jacobi zo traag? (bijvraag: kan je dit grafisch ook verklaren?)
- Bespreek de conditie van de kleinste-kwadratenmethode. Je mag hierbij aannemen dat A van volle rang is.
Examen 29 januari 2007
- veelterm van de vorm (x-2)(x-4)...(x-30). Waarom wordt de fout groter naar gelang een groter nulpunt wordt gekozen.(merk wel op dat naar gelang x->30 dat de fout weer kleiner wordt aangezien ai daar 1 is. Gewoon uitwerken naar f(x) = y(x) + E(x) en dan E(x) afzonderen. Dit geeft |emach| SOM(i=0 ..15) |ai| x^i.
- Zij p(X) een veelterm van onbekende graad zodanig dat p(0) = 4, p(1) = 9, p(2) = 15 en p(3) = 18. Veronderstel dat alle gedeelde differenties van orde 4 gelijk zijn aan 1. Bepaal de coëfficiënt van x^3.
- niet-lineaire vergelijkingen. Je krijgt een stelsel van twee vergelijkingen en de jacobiaan ervan. Bespreek het rare verloop(oorzaak is de singulariteit van de jacobiaan met die startwaarden, dus wanneer de determinant van de jacobiaan gelijk is aan 0, met de berekening van deze determinant kan je bepalen welke startwaarden hier aan voldoen). Verder moet je ook de convergentiefactor en orde geven van de NR methode en de vereenvoudigde NR methodes.
- Je krijgt een matrix A, b en de QR vorm van A. Bereken minx ||Ax - B||. Welke methode gebruik je hiervoor? (kleinste kwadratenbenadering(slides) natuurlijk.)
Examen 8 juni 2007
examenvragen die de industrieel ingenieurs die het overgangsprogramma naar burgie volgen kregen (voor zover 'k het me nog herinner):
- Gegeven :
een fuctie f(x) van de 6de graad x = 1.1 is een nulpunt een hoop matlab-code die ik niet verstond (alle matlab-oefenzittingen gebrost :-s) uit de commentaar was duidelijk dat ze Newton-Raphson toepasten een grafiek waarin duidelijk is dat de fout telkens kleiner wordt tot ongeveer 40 iteratiestappen, en daarna terug omhoog schiet, en terug zacht naar beneden gaat (en zo herhaalt zich dat). (grafiek zag er zo uit \|\|\|\| )
Gevraagd: leg in detail deze grafiek uit kun je een betere methode bedenken?
oplossing : als ge de afgeleide van de gegeven functie berekent, dan is deze voor het opgegeven nulpunt ook nul, net zoals de derde en vierde afgeleide. We hebben dus te maken met een nulpunt met multipliciteit. => gevolg: newton-raphson = 1 - 0/0 Alternatief => Whittaker
- Gegeven:
Veelterm van nen bepaalde graad (5de graad?) De exacte integraal van deze veelterm van -1 tot 1 is een bepaalde waarde (waarde is gegeven) We gaan de integraal bepalen met twee kwadratuurformules. Weer matlabcode (:-s) x1 = -alfa, x2 = 0, x3 = alfa H1, H2 en H3 gegeven
Eerste kwadratuurformule: alfa heeft bepaalde waarde de waarde van de kwadratuurformule is exact de opgegeven waarde
Tweede kwadratuurformule: ander alfa waarde, de rest hetzelfde. de waarde van de kwadratuurfomule geeft nu een andere oplossing dan hierboven
Gevraagd: - kunnen we hieruit besluiten dat de nauwkeurigheidsgraad van de eerste kwadratuurformule beter is dan de tweede? (uiteraard niet... anders zou hij't zo niet vragen :-p) - bereken de nauwkeurigheidsgraad van de kwadratuurforumules
Oplossing: nauwkeurigheidsgraag van eerste was 2 en van tweede 5 (zie oefenzitting 8, opgave 3. en 4., in combinatie met p142 (en daarrond) in handboek)
- Gegeven:
f(x) = x² - x + 1 Weeral matlabcode (:-s) x* = 1 Door middel van substitutiemethodes word deze functie benaderd, ne keer langs links, en langs rechts (ik dacht voor x=0,9 en x=1,1) Twee grafieken gegeven, op de ene (x=0,9) zie je fout kleiner worden, op andere zie je fout groter worden. Verklaar.
Zie dus figuur 2.10 op pagina 221. Bijvraag was iets van convergentiefactor bepalen ofzo
- Gevraagd : wat gebeurd er als we "von Mises" op een matrix A uitvoeren met en een startvector X
A = [ 2 1 -1 | 0 3 -5 | 0 0 -2 ] en X = [ -1 | 1 | 1 ]
antwoord: normaal vinden we met von Mises (= Methode der machten) de grootste eigenwaarde. Nu niet, en dat komt omdat onze startwaarde toevallig een lineaire combinatie is van de twee andere eigenvectoren.
Examen 20 augustus 2007
VRAAG 1: Examenvraag 15
VRAAG 2: Examenvraag 9
VRAAG 3: Beschouw de substitutieformule met a reëel. Voor welke waarden van zijn er één/geen/meerdere vaste punten? Als er een vast punt is, wanneer convergeert de methode dan? Naar welk punt? Voor welke startwaarden? Ken je hiervoor een geschikt stopcriterium?
VRAAG 4: Wat maple code over de methode der machten. Een driehoekige matrix is gegeven, met zijn eigenwaarden 2, 3 en -2. De methode Verder is ook een startvector gegeven. De methode lijkt te convergeren naar 2, maar convergeert tenslotte toch naar 3, dit zie je in een grafiek. Vraag: leg de grafiek uit. (Dit is omdat de startvector kan geschreven worden als een lineaire combinatie van de eigenvectoren van de matrix, en de component van de eigenvector bij 3 is zeer klein.) (Vraag uit een oude examenbundel)
Examen 14 januari 2008 (informatica)
- Examenvraag 5
- Examenvraag 2 (minimale ||r|| bepalen en zeggen hoe je de vector x die daarbij hoort kunt vinden)
- Examenvraag 6
- Maple-sheet met stelsel van 2 niet-lineaire vergelijkingen en bijbehorende Jacobiaan gegeven. Grafieken van gewone newton-raphson en vereenvoudigde NR (enkelvoudige en totale stap methodes) -> Convergentieorde en -snelheid geven van beide methodes.
Examen 14 januari 2008 (1)
Exact hetzelfde examen als op 19 januari 2006.
Examen 14 januari 2008 (2)
Hetzelfde examen als 29 januari 2007.
Examen 18 januari 2008, voormiddag (informatica)
- Examenvraag 11
- Examenvraag 12
- Gegeven de methode van Newton Raphson. Verklaar de relatieve fouten grafiek van een willekeurige 5de graads veelterm met 3 nulpunten.
- Examenvraag 32
Examen 18 augustus 2008, voormiddag (informatica)
Zelfde als het herexamen van 20 augustus 2007.
Examen 8 juni 2009, namiddag
- Examenvraag 4
- Examenvraag 5
- Examenvraag 23
- Examenvraag 24
Examen 9/06/09 voormiddag
- VRAAG 1: zelfde als examenvraag 1 van examen 20 augustus 2007
antwoord: 0.1 wordt binair door een repeterend patroon ofzo voorgesteld en dus als we inlezen wordt er een deel van dat patroon afgebroken en dus een kleine fout gemaakt. een geheel getal zoals 3 kan wel exact worden voorgesteld, en dus wordt de formule met fouten:
fl(x) = 0.1(1+e)
y= 3*x(1+e')(1+e)
fl(y) = y(1+e)
en dus wordt er drie keer een foutje gemaakt en zal y dus niet meer exact gelijk aan 0.3 zijn (dat trouwens ook niet exact kan worden voorgesteld maar ook, zoals x, wordt afgebroken)
bij het uitschrijven van y, wordt de binaire info terug omgezet naar decimaal talstelsel en vermits de fout die wordt gemaakt kleiner is als de machineprecisie zie je die eerst niet.
- VRAAG 2: bereken een derde graad hermite interpolerende veelterm y0011(x) in twee interpolatie punten x0 en x1 met hun afgeleiden. (dus 1 graad hoger als het voorbeeld in boek deel II hoofdstuk 2 sectie 11)
- VRAAG 3: 5de graadsveelterm gegeven en grafiek gegeven en maple printouts van van alles en ook de grafiek van de relatieve fout gegeven met verschillende punten en hun functie waarden uit die laatste grafiek.Gebruikte methode is Newton Rhapson.
gevraagd: bespreek het verloop van deze foutenkromme in detail. Wat is de convergentiesnelheid?
het was kwadratisch verloop, ma hij vroeg nog:" Kunt ge da eigelijk zien in de grafiek dat het kwadratisch is? Het kan toch ook superlineair zijn?"
- VRAAG 4: zelfde als examenvraag 4.
Antwoord: ge berekend dus eerst de eigenvectoren bij de eigenwaarden en dan ziet ge dat de startvector praktisch gelijk is aan een lineaire combinatie van twee eigenvectoren (-2 en 2) en daardoor zit uw iteratie in het begin vast in het vlak van die 2 eigenvectoren. Door de lichte afwijking op de vector (de .00001) komt de vector na genoeg iteraties toch uit het vlak en gaan we naar 3 itereren. Moest de startvector exact een lineaire combinatie van 2 eigen vectoren zijn dan zou men nooit naar 3 convergeren. (zie ook oefenzitting 10, Matlab sessie, daar hebben we ongeveer hetzelfde gedaan) De grafiek van de norm van de gevonden vector is ook gegeven en daar ziet ge dat hij eerst nen tijd op 2 staat en dan pas na 20 stappen begint te schommelen en toch naar 3 gaat. Waarom? Omdat hij pas de afwijking van de ideale waarden (de .00001) gaat zien nadat de iteratieve methode de juiste precisie heeft bereikt. Dat wil zeggen na 20 stappen (1 stap is 1 bit en 3 bits per getal nauwkeurig => 20 stappen voor 6 getallen nauwkeurig)
Examen 15/06/09 voormiddag
- 1) Gegeven: R = AX-B, norm van R, A en B alsook het conditiegetal van A en de diagonaal van L of U van een lu decompositie van A.
- Gevraagd was of X een goede benadering was voor het exacte resultaat
- De determinant van A
- nog 2 kleine vraagjes
- 2) Als we bij voorwaartse differenties een fout aanbrengen op f(k) ter grootte van E.
- Hoe plant de fout zich voort, met welk patroon
- Als we veronderstellen dat de differenties bij hoge graad zeer klein worden kunnen we op het einde van de tabel de grootte van de fout en de plaats van de fout aflezen, verklaar en leg uit.
- 3) Beschouw de substititutiemethode x_(k+1) = exp(x_k).
- Is er convergentie ?
- Voor welke startwaarden ?
- Nog een vraag waar ik niet kan opkomen
- 4) Gegeven hoop maplecode over Newton-Raphson
- Gevraagd wat de convergentiefactor en orde van convergentie
- De laatste grafiek toonde een lineair gedrag. Verklaar waarom de methode traag convergeert.
Examen 15/06/2009 namiddag
Vraag 1 Beschouw de volgende functie
We willen de waarde berekenen van deze functie van x in de buurt van 0. We gebruiken daarvoor het volgend algoritme:
a ↠b ↠f ↠b-1-a
Is dit algoritme stabiel? Geef de waarde van met 10 juist beduidende cijfers.
Vraag 2 Gebruik de Lagrange formule om te bewijzen dat voor -h≤x≤h
met D(x) de differentiefout. Geef een uitdrukking voor D(x).
Vraag 3 Maple prints
a) Verklaar waarom de methode van Newton Raphson in 1 iteratiestap op afrondingsfouten na de exacte oplossing vindt!
b) Wat is de orde van de convergentie en wat is de convergentiefactor?
c) Verklaar in detail waarom de totale stap vereenvoudigde Newton Raphson zo traag convergeert.
Vraag 4 Matlab output
We hebben een random matrix A en een random rechterlid b. De singuliere-waarden-ontbinding van A berekend en de vector bt wordt berekend als
Geef de waarde van
tot op 2 juiste beduidende cijfers.
Geef aan welke methode je zal gebruiken om de vector te berekenen die de hierboven aangegeven 2-norm minimaal maakt.
Examen 16/06/09 namiddag
- 1) Bespreek de conditie van de nulpunten van x^2+2x+c (c<1).
- Mondelinge Bijvraag: is de conditie goed/slecht voor de abolute of relatieve fout?
- 2) Bewijs dat voor voorwaartse differentie geld dat DELTA(f_k/g_k) = [g_k*DELTA(f_k)-f_k*DELTA(g_k)] / (g_k*g_(k+1))
- 3) Beschouw de substititutiemethode x_(k+1) = exp(a*x_k). Voor welke a bestaan er geen/1/meerdere vast punten. Convergeert de methode? Zo ja, naar welke vaste punten? Voor welke startwaarden? Geef een goed stopcriterium.
- Mondelinge Bijvraag: Convergentiesnelheid?
- 4) Newton-Rhapson bij niet-lineair stelsel
Examen 19 juni 2009
Vergelijk met examen 8 juni 2007.
- Gegeven is de functie f(x) = (x - 1,1)^5 (maar uitgewerkt, dus f(x) = x^5 - 5,5*x^4 + ..., en er stond niet bij dat dit gelijk was aan (x-1,1)^5). Er is een Maplecode gegeven waarmee we via Newton-Raphson het nulpunt 1,1 willen bepalen. Men tekent de relatieve fouten en de grafiek daalt lineair, en schiet plots omhoog, daalt weer en terug omhoog, ... \|\|\|... Verklaar wat je ziet in de grafiek en geef een variant van Newton-Raphson waar dit probleem niet opduikt.
- Beschouw waarbij a een parameter is. Definieer . Bewijs dat de interpolerende veelterm van f door 0 = x0, x1, ..., xn gegeven wordt door , en dat de interpolatiefout gelijk is aan .
- We gaan aan de hand van Maple het vast punt 1 van F(x) = x²-x+1 berekenen. We itereren telkens 1000 keer. De eerste keer beginnen we onder 1 (beginwaarde 0,9) en de tweede keer boven 1 (beginwaarde 1,1). De grafieken worden getekend en bij de eerste convergeert het monotoon naar 1 en bij de tweede divergeert het. Verklaar!
- Wat gebeurt er als we de von Mises-methode toepassen op en beginvector ?
Examen 7 juni 2010
- Gegeven de volgende gegevens, kan je hiermee f(x1) uitrekenen?
f[x0,x0,x1,x1] = 1; f´´(x0)=0; f´´(x1)=0; f´(x0)=0; f´(x1)=0; f(x0)=2; x0=0; x1=1;
- Maple code: (beschrijving ervan: er werd van het getal 1000 50 keer de wortel genomen, daarna werd dit getal 50 keer gekwadrateerd. De vraag was dan: bespreek hoe het komt dat deze waarden zo verschillen.
- Gegeven de iteratieformule x(k+1) = (x(k) - a)² - 1, met a > 0. Voor welke reële waarden van a en x(0) is er convergentie, en naar welke waarden van x gebeurt dit? Wanneer treedt er kwadratische convergentie op?
- Gegeven maple code waar methode van de machten werd op toegepast. De gegevens werden erin genormeerd en mu werd uitgezet op de grafiek. Daarop was te zien hoe die convergeerde naar de dominante eigenwaarde. Ook werd er een grafiek gegeven die de relatieve fout van mu (in logaritmische schaal) uitzet tov het aantal iteratiestappen. Die was dalend en in 'rechte'-vorm. Je moest de grafieken bespreken en een bijvraag was hoe je op de laatste grafiek de convergentiesnelheid kon zien.
Examen 18 juni 2010 namiddag
- oefening uit de eerste oefenzitting
- Zij A een matrix waarbij alle elementen nul zijn, behalve die op de diagonaal en die op de antidiagonaal. Schrijf een algoritme om het stelsel AX=B op te lossen, met B een gegeven vector. Bereken de hoeveelheid rekenwerk.
- Maple code: niet-lineair stelsel, Newton-Raphson, Grafiek van de twee functies en de benaderingen van het snijpunt, grafiek van de relatieve fout tov aantal iteratiestappen. Hoe snel convergeert de metode? Verklaar in detail. Wat is de orde van convergentie en de convergentiefactor? Waarom convergeert de methode in dit geval zo snel/traag? Verklaar dit in detail. Bij welke startwaarden of tussenpunten stopt de methode?
- A= met , , , . Hierop voeren we de methode van de machten uit. Bepaal de orde van convergentie en de convergentiefactor. Bij de benadering van de dominante eigenwaarde bereiken we slechts een beperkte nauwkeurigheid (emach=). Verklaar dit in detail.
Examen 10 juni 2011 voormiddag
Exact hetzelfde als het examen van 19 januari 2006.
Examen 17 juni 2011 (Informatica)
1) 2x2-matrix A met zeer grote getallen (orde 10^40 enz) en matrix B. 2 benaderende oplossingen voor stelsel Ax = B gegeven, met verschillende methodes berekend (er is niet gegeven welke methodes). Vraag: zeg iets over de stabiliteit van de gebruikte methodes
2) veelterm p(x) met p(-1) = p(0) = p(1) en p'(0) = 1. Geef alle veeltermen van zo laag mogelijke graad die hieraan voldoen. Antwoord: via methode der onbepaalde coëfficiënten: p(0)+x-x³
3) maple-output voor het zoeken van een nulpunt van een veelterm. De veelterm, zijn grafiek en zijn afgeleide zijn gegeven. de methode van newton-raphson wordt gebruikt. Op de grafiek zien we dat de relatieve fout lineair daalt. Vraag: waarom is de convergentie zo traag? wat zegt dit over het nulpunt? geef de convergentiefactor. waarom zijn slechts 7 van de cijfers van de benaderende oplossing juist, terwijl we over 16 cijfers beschikken? Bijvraag: kan je de convergentiefactor grafisch tonen op de grafiek? Antwoord: trage konvergentie want meervoudig nulpunt. Meervoudigheid was 3 dus konvergentiefactor 2/3. Slechte benadering want slecht geconditioneerd probleem.
4) gegeven: A = compagnion-matrix (zie laatste schriftelijke oefenzitting), kies een willekeurige startvector X(0). for(i=1..n) { X(i) = A*X(i-1); scaleer X(i) zodat het laatste element van deze vector 1 wordt; }. Vraag: toon aan dat het voorlaatste element van de vector X(n) konvergeert naar de (strikt) grootste eigenwaarde.
Examen 24 juni 2011 namiddag
Hetzelfde examen als 8 juni 2007 met als enige verschil vraag 2:
2) Gegeven enkele equidistante punten Xi, f(Xi). Er staat een fout epsilon op 1 van die punten, namelijk op Xk, f(Xk). Als je de tabel van voorwaartse (=gedeelde) differenties opstelt kan je zien hoe de fout zich propageert. Herken je een bepaald patroon? (duh, anders zou hij het niet vragen) Je mag er van uit gaan dat de differenties met hogere graad naar 0 gaan. Hoe kan je vinden op welk punt Xk de fout zat en hoe groot die is?
oplossing: Stel gewoon een tabel op voor N elementen:
X1 f(X1) ... Xk-2 f(Xk-2) Xk-1 f(Xk-1) Xk f(Xk)+epsilon Xk+1 f(Xk+1) Xk+2 f(Xk+2) ... Xn f(Xn)
en reken die dan een paar stappen uit. Je zal zien dat de fout epsilon groter wordt en zich uitbreidt. Ook wisselt de fout steeds van teken: dit komt omdat als je de gedeelde differenties uitrekent, je soms -(f(Xk)+epsilon) moet doen, wat de epsilon negatief maakt. Als je vervolgens nog eens moet aftrekken, -(f(Xk)-epsilon) dus, dan wordt epsilon weer positief. Uiteindelijk bekom je volgend patroon in de fouten, dat eigenlijk de driehoek van pascal/binonium van newton is!
eps
eps
eps -4*eps
eps -3*eps
eps -2*eps 6*eps
-eps 3*eps
eps -4*eps
-eps
eps
enzoverder. De fout verbreedt dus, maar de tabel wordt kleiner. Uiteindelijk zal je dus met 1 getal overblijven (want de f(x)'en worden allemaal 0 als je blijft doorrekenen. Stel dat dat getal bijvoorbeeld -10*eps is. Je zoekt in de driehoek van pascal op waar die "10" staat, en zie je dat op de 6e rij staat tussen 1 5 10 12 10 5 1. De 10 staat op de 3e plaats links, maar ook op 3e plaats rechts. Dit komt overeen met k of n-k = 3, dus het punt waar de fout op zit staat op derde plaats in de tabel OF op de n-3 plaats.
Examen 11 juni 2012 voormiddag (Informatica)
Vraag 1: We hebben de volgende gegevens van de functie .
Kunnen we met behulp van deze gegevens de waarde van de functie bepalen in , d.w.z., ?
Oplossing:
Vraag 2: Er is maple code gegeven die er ongeveer zo uit ziet:
- x = 1000
- for(1 to 50)
- x = sqrt(x);
- end
- for(1 to 50)
- x = x*x;
- end
- x
De output is
- x = 1000
- x = 1009 (Denk ik, toch iets in die buurt.)
Verklaar in detail waarom deze waarden zo verschillen.
Oplossing:
Werk dit uit met de notatie.
Bijvraag: Zal er na de 50 worteltrekkingen ook al een relatief grootte fout te zien zijn?
Vraag 3: Zij het iteratieproces voor gegeven. Voor welke reële waarden van en is er convergentie naar een reële waarde ? Wanneer treedt er kwadratische convergentie op?
Oplossing:
met voor
=>
Er is convergentie als
dus dus
Er is kwadratische convergentie als dus als dus als .
Vraag 4: Methode der machten
en
Omdat de matrix A bovendriehoeks is, vinden we de eigenwaarden van A op de hoofddiagonaal: 9, 10, 8. De dominante eigenwaarde is dus 10. Er wordt maple code gegeven om die de methode der machten toepast met normalisatie. De methode wordt 100 keer uitgevoerd met k = 1..100. Er wordt een grafiek gegeven van elke benadering van (=10) voor elke iteratie. Er wordt ook zo'n grafiek gegeven voor de relatieve fout.
Verklaar de grafieken die hierboven gegenereerd werden. Wat is de orde van convergentie en wat is de convergentiefactor? Wat zou er gebeuren als we in de methode hierboven geen normalisatie zouden gebruiken? Bijvraag: kan je de convergentiefactor ook afleiden uit de 2 grafiek?
Oplossing:
De orde is lineair (dit is altijd zo bij de methode der machten)
De convergentiefactor is
De methode der machten is enkel geldig als . halen we uit en vinden we door
Uit halen we dat Dus de methode der machten mag gebruikt worden met startvector
Als we geen normalisatie zouden gebruiken zouden we overflow krijgen.
Examen 22 juni 2012 voormiddag
Examenvraag 28 t/m 31 (hij vraagt ze zelfs op volgorde!)
Examen 10 juni 2013 (9u00)
- Bespreek de conditie van de nulpunten van met . Is de conditie goed/slecht voor de abolute of relatieve fout?
- Gegeven . Bereken , en zodat maximaal is.
- Beschouw de substititutiemethode . Voor welke a bestaan er geen/1/meerdere vast punten. Convergeert de methode? Zo ja, naar welke vaste punten? Voor welke startwaarden? Geef een goed stopcriterium.
- Newton-Rhapson bij een niet-lineair stelsel vergelijkingen.
Examen 11 juni 2013 (14u00)
- Gegeven . Bereken de waarden van de gewichten zodat de nauwkeurigheidsgraad maximaal is, hoeveel is deze nauwkeurigheidsgraad?
- Gegeven . Wanneer is het probleem van het zoeken van dit nulpunt goed geconditioneerd? Hoeveel gaan de nulpunten verschuiven bij een verschuiving van ?
- Beschouw de substititutiemethode . Treedt er convergentie op? Zoja, wat zijn de convergentiefactor, convergentiesnelheid en convergentie-orde?
- Gegeven de matrix , en We passen de methode van Jacobi toe op deze matrix. Bepaal de convergentiefactor en de convergentie-orde. Waarom is er een trage convergentie? Geef grafisch weer hoe er geconvergeerd wordt.
Examen 23 augustus 2013 (8u00)
Vraag 1: (Oefenzitting 2, Probleem 6), enige verschil staat vetgedrukt.
We weten dat . We gaan de waarde benaderen door uit te rekenen voor
- and
- .
In de figuren hieronder geven we de relatieve fout weer, d.w.z. . De eerste figuur geeft de relatieve fout voor de machten van 2 terwijl de tweede figuur de fouten voor machten van 10 weergeeft.
(figuur)
Waarom zijn de twee grafieken zo verschillend? Doe hiervoor voor beide gevallen een foutenonderzoek. Kan men hieruit afleiden met welke basis en met hoeveel beduidende cijfers de computer werkt? Verklaar in detail je antwoord.
Vraag 2:
Bepaal de Hermite interpolatie die de functiewaarden en de eerste afgeleiden in en interpoleert. (Geen waarden gegeven.)
Bepaal de interpolatiefout.
Vraag 3: (MATLAB)
- Data:
- Een veelterm van graad 5.
- De afgeleide van de veelterm.
- MATLAB:
- Code voor Newton-Rhapson.
- Figuren:
- Grafiek van de veelterm.
- Log-plot van de relatieve foutentermen.
We zien dat deze veelterm nulpunten heeft in , en . We gebruiken Newton Rhapson met en k = 100.
Waarom convergeert deze zo traag? Kunnen we hier iets uit afleiden over het gezochte nulpunt?
Kunnen we uit de foutenplot de convergentie factor afleiden? Kunnen we hier iets uit afleiden over het gezochte nulpunt?
We werken in een machine met 16 beduidende cijfers. Waarom is de gevonden oplossing zo onnauwkeurig?
Vraag 4:
Matrix A (3x3, gegeven).
We gebruiken de methode van de machten met startvector . Deze levert eigenvector (gegeven) horende bij eigenwaarde .
Dit proces herhalen met startvector levert , wederom met eigenwaarde . is nochtans geen veelvoud van .
Verklaar in detail.
Examen 10 juni 2016 (namiddag)
Examen 15 juni 2016 (8u00)
- Men probeert e te benaderen via de formule (1 + 1/x)^x voor grote x. Men gebruikt als x'en zowel 2^k als 10^k. Gegeven grafieken voor de relatieve fout ten opzichte van k voor de twee methoden. Verklaar het verschil in de grafieken, wat is de basis van de machine waarop het uitgevoerd werd, hoeveel beduidende cijfers in die basis gebruikt ze? Mondeling vroeg hij wel waarom de relatieve fout bij de 10^k-methode minimaal 10^-8 wordt, ongeveer de helft van de beduidende decimale cijfers ondersteund door de machine.
- Ontwerp een algoritme dat een lineair stelsel oplost waarbij de coëfficiëntenmatrix alleen niet-nul-elementen heeft op de diagonaal en antidiagonaal (linksonder naar rechtsboven). Hoeveel rekenwerk vraagt je algoritme? (Niet exact, Big-O notatie volstaat.)
- Gegeven de functie f(x) = (1 - sin(x))/cos(x). De limiet van f(x) naar pi/2 is 0. Dit "nulpunt" (bestaat technisch gezien niet) wordt benaderd met de bisectiemethode, Maple-code gegeven. Je krijgt ook als Maple-output een grafiek van de relatieve fout ten opzichte van het aantal iteraties.
- Kan je uit de grafiek de convergentiesnelheid (lineair, kwadratisch, superlineair, ...), convergentieorde en convergentiefactor afleiden? Komt dit overeen met de theorie?
- Is dit probleem slecht geconditioneerd?
- De relatieve fout blijft "vast hangen" rond 10^-9, terwijl de benadering uitgevoerd wordt met 20 beduidende decimale cijfers. Verklaar.
- Gegeven de matrix A = [[7, 2, 10], [-1, 4, -5], [-1, -1, 0]]Men past de methode van de machten toe (met scalering) met als startvector [1, 0, 0]^T, en komt voor de eigenwaarde 5 de eigenvector X1 uit. Bij startvector [0, 1, 0]^T komt men voor dezelfde eigenwaarde de eigenvector X2 uit. X1 ~ [0.9733, -0.1622, -0.1622]^T en X2 ~ [0.5345, 0.8018, -0.2673]^T Deze vectoren zijn geen veelvoud van elkaar. Hoe kan dit? Verklaar met detail. Mondeling vroeg hij nog wat het concrete verband is tussen de uitkomstvector en de startvector.
Examen 15 juni 2017 (NM)
Examen 16 juni 2017 (NM)
Examen 19 juni 2017 (NM)
Examen 18 augustus 2017 (VM)
Examen juni 2018
Examen 11 Juni 2019 (08u)
Examen was uitzonderlijk niet mondeling.
Vraag 1
Drie vragen oplossen op max 1 pagina.
a) Methode van de Machten voor Bovendriehoeksmatrix
Naar welk getal convergeert de methode van de machten?
b) Interpolatie
Zal de fout op een willekeurig punt dalen als meer interpolatiepunten worden toegevoegd.
c) Machinefout
Kan correct voorgesteld worden op een computer (IEEE standaard).
Vraag 2: Numerieke integratie
Bepaal de coëfficiënten en nauwkeurigheidsgraad. Herken je de formule?
Vraag 3: Conditie stelsel lineaire vergelijkingen
Conditiegetal van a = 4*10^5
Maak een schatting van het verschil, is deze betrwoubaar.
Vraag 4: Substitutiefuncties
Gegeven 2 tabellen die convergeren naar -0,02, welke hoort bij welke substitutiefunctie. Bepaal de convergentiefactor met behulp van de tabel (als dit zinnig is).
Een andere tabel die start bij 0,2 en convergeert naar 0,25 met . Bepaal de convergentiefactor en verklaar.
Examen 14 juni 2019
Examen 18 juni 2019 (8u)
Vraag 1
Drie vragen oplossen op max 1 pagina.
a) Stel dat de afgeleide van de functie in wordt benaderd door .
Kies je h best (a) gelijk of (b) groter of (c) kleiner dan ? Waarom?
b)
Stel we gebruiken de methode van Newton om het nulpunt van een functie te berekenen met .
Teken in de omgeving van het nulpunt waarvoor het stopcriterium te optimistisch is (m.a.w. waar het te vroeg stopt.)
c)
Naar welk getal convergeert de methode van de machten? Waarom is dat zo en hoe kom je hierop?
Vraag 2 Stel je moet een computerprogramma schrijven dat benadert met minimaal 6 juiste cijfers. Enkel +, -, x en / mogen gebruikt worden.
Leg gedetailleerd stap voor stap uit hoe je te werk gaat. Let op: de sinusfunctie mag wel uitgevoerd worden om het programma af te leiden, maar mag niet in het programma zelf gebruikt worden uiteraard.
Vraag 3
Gegeven een ijle matrix A waarvoor alleen niet nul zijn. (in de rijen 1, 2 en N-1, N bestaan de elementen die erbuiten vallen natuurlijk gewoon niet --> zie 'bandmatrix')
Stel dat je dit oplost met de methode van Gauss-Seidel en je in iteraties de gevraagde nauwkeurigheid bereikt. Hoeveel rekenkundige bewerkingen (+, -, *, /) worden er uitgevoerd? Vergelijk dit aantal met LU-factorisatie waar er geen rekening wordt gehouden met het ijle karakter van de matrix.
Vraag 4
met
We gebruiken bovenstaande formule om de nulpunten van te berekenen. Je kan onder redelijke voorwaarden kwadratische convergentie verwachten.
1) Bewijs dat dit geldt.
2) Is er een voordeel t.o.v de methodes die we in de cursus hebben gezien?
Antwoord op 20 lijnen
Examen 24 juni 2019 (8u)
Examen 24 juni 2019 (13u)
Examen 03 september 2019 (8.30u)
Examen 11 juni 2020 (8u)
Examen 12 juni 2020 (12u)
Examen 12 juni 2020 12u (Eigen uitgewerkte antwoorden)
Examen 15 juni 2020
Examen 22 juli 2020
Examen 17 juni 2021
Examen 21 juni 2021
Vraag 1
(zelfde vraag als op het examen van 12 juni 2020)
Gegeven dat
a) Geef de conditie van (ook voor ).
b) Geef de stabiliteit van de oplossingsmethode (ook voor ).
Vraag 2
(zelfde vraag als op het examen van 12 juni 2020)
Bepaal de gewichten voor volgende kwadratuurformule zodat de nauwkeurigheidsgraad maximaal is:
Wat is deze nauwkeurigheidsgraad?
Vraag 3
Gegeven dat ,
a) Geef de vaste punten van .
b) Convergeert dit? Indien dit het geval is, wat is dan de convergentiesnelheid? Indien deze lineair is, geef dan ook de convergentiefactor. Geef ook de orde van elk punt. (niet meer zeker van de exacte bewoording van de prof.)
c) Voor welke startpunten convergeert dit? Leg uit en maak ook een grafiek waarop je voor verschillende karakteristieke punten schetst hoe ze convergeren. (ook hier niet zeker hoe het er exact stond, maar de essentie is hopelijk wel duidelijk)
Schakelprogramma Master (Toegepaste) Informatica
Examen 10 juni voormiddag/17 augustus voormiddag
Vraag 1
We lossen met een bepaalde methode het stelsel AX=B op. We krijgen de berekende vector Y als benadering voor X. Hieronder volgt een gedeelte van de bijbehorende Matlab-sessie:
>> R=A*Y-B;
>> norm(R)
ans = 4.4409e-15
>> norm(A)
ans = 1.4281e+01
>> norm(B)
ans = 4.3197e+01
>> cond(A)
ans = 4.0892e+11
>> [L,U] = lu(A);
>> diag(U)'
ans =
Columns 1 through 5
1.2618e+00 1.0839e+00 1.5534e+00 1.9028e-10 -8.1081e+01
Columns 6 through 10
1.8780e+00 1.7355e+00 1.5833e+00 -9.5583e-01 -1.7088e-01
- Hoe nauwkeurig is de berekende oplossing Y?
- Is de berekende oplossing Y van het probleem een exacte oplossing van een nabijgelegen probleem?
- Kan je de determinant van A berekenen?
Zo ja, geef dan een benaderende waarde. - Kan je berekenen?
Vraag 2
Bepaal de gewichten in de kwadratuurformule
zodanig dat de naukeurigheidsgraad zo hoog mogelijk is.
waarbij f' een notatie is voor de afgeleide van f.
Vraag 3
Beschouw de substitutieformule
.
Ga na of er convergentie is. Voor welke startwaarden? Ken je een goed stopcriterium hiervoor?
Vraag 4
Zoals examenvraag 3: http://people.cs.kuleuven.be/~marc.vanbarel/NumWis/Illus/Zeros2/STELSELS1.html, maar dan met de volgende gegevens:
u = x² + (y-2)²-3.7 v = x² + y² - 4 (matrix J is 2x 2y-4; 2x 2y)
- a) Verklaar waarom de tweede en volgende iteraties bij Newton-Raphson op een horizontale lijn gelegen zijn.
- b) Voor welke startpunten (en tussenliggende punten) werkt de methode van Newton-Raphson niet.
- c) Wat is de orde van convergentie en wat is de convergentiefactor?
- d) Wat is de orde van convergentie en wat is de convergentiefactor?
- e) Verklaar in detail waarom de totale stap vereenvoudigde Newton-Raphson zo traag convergeert.
Examen 30 juni 2022
Vraag 1 Beschouw de functie f(x) = (x²-1)-(x+1) Matlab functie: (x.x-1)-(x+1)
Vraag a) Bespreek de conditie van het probleem ten opzichte van de relatieve fout voor een willekeurige waarde van x
Vraag b) Bespreek de numerieke stabiliteit van de berekeningsmethode voor een willekeurige waarde van x
Vraag 2 gegeven: x1 - x0 = 1 f(x0) = 1 f(x1) = 2 f'(x0) = -1 f[x0, x0, x1, x1] = 4
zoek f'(x1)
Vraag 3 Beschouw de functie f(x) = x³ - 4x² + 4x waarvan we de nulpunten gaan benaderen met de methode van Newton-Raphson.
Vraag a) Bepaal de bijhorende functie F(x).
Vraag b) Zijn er vaste punten? Zo ja, bereken elk van deze vaste punten.
Vraag c) Ga voor elk vast punt na of er lokale convergentie is naar dit vast punt? Zo ja, wat is de convergentiesnelheid (lineair, superlineair, kwadratisch, . . . )? Als de convergentiesnelheid linear is, geef dan ook een numerieke waarde voor de convergentiefactor. Komt dit ook overeen met wat je theoretisch weet over de convergentiesnelheid van de methode van Newton-Raphson? Vraag d) Voor welke startwaarden is er convergentie, voor welke startwaarden is er divergentie? Staaf je antwoord op deze vraag op een grafische manier door voor verschillende karakteristieke gevallen van de startwaarde een schets te maken van het iteratieproces.
voorbeeldexamen
Media:Voorbeeldexamen-numerieke.pdf - Oplossingen vind je onder: https://drive.google.com/open?id=1-B0Yyv4DDNyFGW6-vjMv-jtfVWmB9-7_
Mogelijk nuttige documenten
Media:Splines_en_Differenties.pdf: Een aantal stellingen en inzichten ivm. B-Splines en gedeelde differenties. Geloven op eigen risico.