Algemene Natuurkunde I

Eerste zit 2004-05, versie 1

Bron: Toledo

Mondelinge vraag 1

Wat verstaan we onder "impuls" of "hoeveelheid van beweging" (Engels: lineair momentum)? Kan dit een behouden grootheid zijn? Wat is het verband tussen "krachtstoot" (Engels: impulse) en "hoeveelheid van beweging"?

Mondelinge vraag 2

Stel een uitdrukking op voor de voortplantingssnelheid van een golf op een snaar.

Oefening 1

Een astronaut is net geland op een planeet waarvan de valversnelling onbekend is. Tijdens een eerste wandeling staat hij op de rand van een ravijn met onbekende diepte. Hij laat een stuk steen uit stilstand in de ravijn vallen en ziet hoe het precies 4,15 seconden later de bodem van de ravijn bereikt. Vervolgens gooit hij een ander stuk steen recht omhoog: het gaat eerst 2 meter omhoog en valt dan ook in de ravijn. Het bereikt de bodem 6,30 seconden na het vertrek. Hoe diep is de ravijn? Moest de astronaut zonder beginsnelheid in de ravijn vallen, met welke snelheid zou hij op de bodem terechtkomen?

Oefening 2

Uit een fontein met de spuitmond op grondhoogte spuit water verticaal omhoog tot een hoogte van 37 m en het debiet is 51,0 liter/seconde. (a) Bereken de oppervlakte van de spuitmond. (b) het water voor de fontein wordt door een pomp aangevoerd van uit een rivier die 100 m lager ligt dan de spuitmond. Als alle verliezen door wrijving verwaarloosbaar zijn, welk vermogen moet de pomp dan leveren om de fontein aan de gang te houden? (Water heeft een massadichtheid van 1 kg/liter.)

Eerste zit 2004-05, versie 2

Bron: Toledo

Mondelinge vraag 1

Bespreek de beweging van een massa aan een veer zonder wrijving en zonder aandrijvende kracht. Bespreek ook de energie van zo'n systeem.

Mondelinge vraag 2

Leid de wet van Bernoulli voor een stromende vloeistof af.

Oefening 1

Als training bij het kleiduifschieten worden er houten blokken in de lucht gegooid en het is de bedoeling deze blokken met een geweerkogel te raken op de top van hun baan. Een blok met een massa van 0,80 kg heeft op de top van zijn baan een snelheid van 10 m/s en wordt geraakt door een kogel waarvan de massa 5,00 g is. Op het moment van inslag heeft de kogel een snelheid van 550 m/s die een hoek van 60° met de horizontale maakt. De kogel blijft in het blok steken. Wat is de snelheid van het blok onmiddellijk na de inslag?

Oefening 2

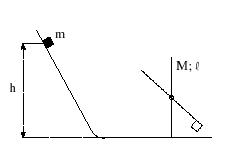
Een blokje (als puntvormig te zien) schuift over een helling naar beneden over een hoogteverschil h en beweegt dan over een horizontaal vlak. Daar botst het tegen het uiteinde van een staaf met lengte 5 en massa M die kan draaien rond een as door het centrum. Bij de botsing blijft het blokje aan de staaf kleven. Met welke hoeksnelheid begint de staaf te draaien? Verwaarloos alle wrijving. (Het traagheidsmoment van een staaf met lengte l en massa M is $\frac{M{l}^2}{12}$ t.o.v. een as door het centrum en $\frac{M{l}^2}{3}$ t.o.v. een as door een uiteinde, als de as loodrecht op de staaf staat.)

Eerste zit 2005-06, versie 1

Wiskunde, reeks 1

Mondelinge vraag 1

Geef de definitie van massacentrum, en bespreek de beweging van een systeem van deeltjes aan de hand van het begrip massacentrum.

Mondelinge vraag 2

Bespreek periodieke geluidsgolven volledig. Toon hierbij duidelijk de verbanden en bespreek ook de verschillen tussen ``verplaatsingsgolven" en ``drukgolven".

Oefening 1

Een blok met massa $m_1=3.00$ kg ligt op een kort hellend vlak met hellingshoek $\alpha =37^{\circ }$. Het blok is met een touw verbonden aan een blok met massa $m_2=2.50$ kg dat verticaal kan bewegen (langs de ``verticale kant" van de helling). Hierbij loopt het touw over een katrol met een verwaarloosbare massa (zonder wrijving). De wrijvingsco\"{e}ffici\"{e}nt tussen het blok met massa $m_1$ en het hellend vlak is gelijk aan $0.10$. Bepaal de versnelling van de blokken en de spankracht in het touw.

Oefening 2

Een komeet beschrijft een hyperbolische baan rond de zon. De snelheid van de komeet bedraagt $v_0$ op een tijdstip wanneer de komeet zeer ver van de zon verwijderd is, en de kortste afstand van het middelpunt van de zon tot de drager van de snelheidsvector is op dat moment gelijk aan d. Bepaal nu de kortste afstand tot (het middelpunt van) de zon die de komeet bereikt op zijn baan in functie van $v_0$, d, G en M. (Hierbij is $G$ de universele gravitatieconstante en M de massa van de zon.)