Deeltjesfysica

Informatie over het examen

Het vak is opgesplitst in twee delen (het eerste door prof. Severijns, het tweede door prof. van Proeyen), en het examen dus ook. Beide proffen zijn de vriendelijkheid zelve op het examen. Elke prof ondervraagt 1 vraag mondeling. De rest is schriftelijk. Het is mogelijk om verduidelijking te vragen over een vraag die schriftelijk opgelost moet worden tijdens de mondelinge ondervraging.

Examens

Academiejaar 2011-2012

30 augustus 2012 (VM)

Examen 30 augustus 2012

11 juni 2012

Examen 11 juni 2012 (deel Severijns) en deel Van Proeyen

Academiejaar 2010-2011

Donderdag 30 juni 2011

Deel Severijns

1. Discuss the following graph (how did one come to this graph?, what is the meaning of it?, etc.) ([1])
2. Are the following reactions possible? If yes, explain why and how the reaction occurs. If no, explain why. De quarkstructuur was gegeven.
   • ${\mathrm{\Lambda }}_c^{+}\to {\mathrm{\Lambda }}^0+e^{+}+{\nu }_e$
   • $pp\to {\mathrm{\Sigma }}^{+}{K}^{+}$
   • ${\mathrm{\Omega }}^{-}\to {\mathrm{\Xi }}^0{e}^{-}\overline{{\nu }_e}$
   • $\pi +\bar{p}\to K^0{\mathrm{\Lambda }}^0$
   • ${\nu }_{\mu }p\to {\mathrm{\Lambda }}_c^{+}{\mu }^{-}{\pi }^{+}{\pi }^{-}$
   • $N\gamma \to e^{-}{e}^{+}$ Hierbij is N een kern.
3. • Explain the difference between electromagnetic and hadronic calorimeters.
   • Discuss vacuum polarisation.
4. • Draw the possible Feynman diagram for $n\to p{e}^{-}\overline{{\nu }_e}\gamma$
   • Draw the Feynman diagrams for the following reactions. Are they leptonic, hardronic, semi-hadronic? Charged or Neutral currents?
     • $K^{+}\to {\pi }^{+}{\pi }^{+}{\pi }^{-}\gamma$
     • $D^{+}\to K^{-}{\pi }^{+}{e}^{+}{\nu }_e$
     • $K^{+}\to {\mu }^{+}{\nu }_{\mu }$
     • ${\nu }_{\tau }{\mu }^{-}\to {\tau }^{-}{\nu }_{\mu }$
     • $B^{-}\to p\bar{p}{\pi }^{-}$

Deel Van Proeyen

1. (mondeling) Consider the process $e^{-}{e}^{+}\to {\mu }^{-}{\mu }^{+}$ Which Feynman diagram (without loops) can be drawn? Write the matrix element for the diagram(s) that you drew.
2. Short questions
   • How many physical states does a photon of a definite 4-momentum $p_{\mu }$ have?
   • How can you see this from the equations describing a photon?
   • Is this different for a Z-boson?
   • And for a gluon?
   • If there were 4 colours, how many gluons would there be?
   • If there were 4 falvours, how many gluons would there be?
   • Suppose that there is a gauge group with 24 indepenent symmetries and we find a set of 20 real scalar fields such that the scalar potential has minima that are invariant under only 8 of these symmetries. Using the Brout-Englert-Higss mechanism, how many physical fields are there that are
     • massive spin 1
     • massless spin 1
     • Goldstone scalars
     • Higgs scalars

Vrijdag 17 juni 2011

Deel Severijns

1. (mondeling) Bespreek CP-violatie bij de kaonen.
   • Een aantal vervallen: bespreek of ze gaan. Zo ja, welke interactie en waarom. Zo nee, waarom niet?
     • $n\to p\overline{{\nu }_e}{e}^{-}\gamma$
     • ${\tau }^{-}\to e^{-}\overline{{\nu }_e}\overline{{\nu }_{\mu }}$
     • ...
   • Je moest van een aantal deeltjes (pionen, neutronen, neutrino's, tau-deeltjes, muonen, elektronen, protonen) zeggen in of ze in een meetbaar signaal achterlieten in de vertexdetectoren, de tracking chamber, de elektromagnetische calorimeter, de hadroncalorimeter en de muon chamber.
   • Weet ik niet meer.
2. Vergelijk de drift chamber met de Time Projection Chamber (TPC). Je kreeg enkele eigenschappen om ze met elkaar te vergelijken (o.a. elektrisch veld; draden in het meetapparaat; dimensies; manier van positie bepalen)
3. Geef de zwakke-interactie-Feynmandiagrammen van de volgende vervallen. En zeg of ze leptonisch, semi-leptonisch of hadronisch zijn.
   • $n\to p\overline{{\nu }_e}{e}^{-}\gamma$
   • ... (ook een aantal tricky overgangen, met meerdere mesonen als eindproducten)

Deel Van Proeyen

1. (mondeling) Als je het volgende deel in je Langragiaan had, hoe ziet de vertex er dan uit. Teken deze en reken het matrix-element uit. ${ℒ}=g\overline{\psi }{\gamma }^{\mu \nu }\psi F_{\mu \nu }$
2. We gaan het matrixelement van de interactie tussen het proton en het elektron uitrekenen. Dit gaat van de volgende vorm zijn: $|{ℳ}{|}^2=\frac{g_e^2}{q^4}{L}_{elektron}^{\mu \nu }{K}_{\mu \nu }$ Hierbij is $K_{\mu \nu }=K_1{g}_{\mu \nu }+K_2{p}_{2\mu }{p}_{2\nu }+K_3{q}_{\mu }{q}_{\nu }+K_4(p_{2\mu }{q}_{\nu }+p_{2\nu }{q}_{\mu })$ en $L^{\mu \nu }=2[p_1^{\mu }{p}_3^{\nu }+p_1^{\nu }{p}_3^{\mu }+g^{\mu \nu }(m^2-p_1\cdot p_3)]$. De inkomende impuls van het elektron is $p_1$, de uitgaande impuls van het elektron is $p_3$ en de inkomende impuls van het proton is $p_2$. (en $q=p_3-p_1$)
   • Bewijs dat $L^{\mu \nu }{q}_{\nu }=0$.
   • Geef de massa-dimensie van $K_i$ (Je weet dat $[{ℳ}]=4-E$, met E het aantal uitgaande lijnen).
   • Toon aan dat $K_3$ en $K_4$ niet uitmaken bij de berekening van het matrix-element.
   • Als $E$ en $E^{\prime }$ veel groter dan $m$ en $p_1=(E,E\widehat{p_1}),p_3=(E^{\prime },E^{\prime }\widehat{p_3})$, wat is dan de grootte van $\widehat{p_i}$?
   • Als $\widehat{p_1}\cdot \widehat{p_3}=\cos \theta$, toon dan aan dat $|{ℳ}{|}^2=\frac{g_e^2}{4E{E}^{\prime }{\sin }^4\frac{\theta }{2}}[-2K_1{\sin }^2\frac{\theta }{2}+K_2{M}^2{\cos }^2\frac{\theta }{2}]$. Wat is M?
   • Tips bij 5:
     • Toon aan dat $p_1\cdot p_3=2E{E}^{\prime }si{n}^2\frac{\theta }{2}$
     • Wat is $q^2$ als $m=0$?

Academiejaar 2009-2010

Vrijdag 25 juni 2010

Deel Van Proeyen

Examen 25 juni 2010 (Van Proeyen)(1/2) en Examen 25 juni 2010 (Van Proeyen)(2/2)

Vrijdag 11 juni 2010

Deel Severijns

1. • Bespreek 'strange particles'. Vanwaar de naam? Hoe in verband brengen met substructuur hadronen?
   • Hoe breng je dit in verband met de Cabbibo-Kobayashi-Maskawa matrix?
2. • 5 reacties waarvan je moet geven of ze al dan niet mogelijk zijn. Indien mogelijk moest je zeggen welke interactie, en waarom. Indien niet mogelijk ook verklaren waarom.
   • Vraagje over de recent ontdekte tau-neutrino's in een bundel zuivere muon-neutrino's (neutrino oscillaties). Je moest een aantal gegeven reacties $p+Be\to {\pi }^{+}+{\pi }^0+{\pi }^0$, ${\nu }_{\tau }+p\to {\tau }^{-}+X^{\prime }$, ${\pi }^{+}\to {\mu }^{+}+{\nu }_{\mu }$ en ${\nu }_{\mu }+p\to {\mu }^{-}+Y^{\prime }$ met X' en Y' niet-relevante andere deeltjes, hierbij in de juiste volgorde zetten (en zeggen welke reacties bvb niet gelijktijdig kunnen optreden enzo). Ook uitleggen waarom je zeker wist dat er een mu-neutrino naar een tau-neutrino was geoscilleerd.
   • Sorteer van binnen naar buiten bij een detector zoals ATLAS. Verklaar ook waarom die volgorde.
     • Vertex
     • Tracking detector
     • Hadron calorimeter
     • EM calorimeter
     • Muondetector
3. 5 reacties met de zwakke interacties gegeven. Feynmandiagrammen tekenen en zeggen of het leptonic, semi-leptonic of hadronic is en of het charged-current of weak-current is.

Deel Van Proeyen

Examen 11 juni 2010 (Van Proeyen)

3 september 2009

Deel 1 (Severijns):

Vraag 1:

• Wat zijn vreemde deeltjes
• Waarom wordt in een reactie zoals (twas een die een s quark omzet in een u) vreemdheid niet behouden. Betrek hierbij de Kobayashi Maskawa matrix

Vraag 2:

• Geef aan via welke interacties volgende reacties plaatsvinden en waarom
• Vul aan met de nodige (anti)neutrinos

de reacties weet ek ni meer, maar je hebt toch al een idee...

Vraag 3: Vergelijk de werking van de cyclotron en de synchrotron

Vraag 4: Enkele Feynmandiagramma. Je moest ook aangeven of het hadronisch/(semi)leptonisch was en of het via geladen of neutrale stroom ging

Deel 2 (Van Proeyen):

• Media: Deeltjes1.png
• Media: Deeltjes2.Png

26 juni 2009

Deel 1 (Severijns):

Weet ik niet meer...

Deel 2 (Van Proeyen):

Vraag 1: (mondeling)

Schrijf neer wat de structuur zou zijn van de volledige Lagrangiaan van het standaard model. Je moet deze niet in detail neerschrijven, maar wel duidelijk maken welke termen er allemaal nodig zijn. Deze vraag komt zeker in de discussie aan bod. Dus je kan je antwoord dan verduidelijken en ik zal het wel vragen als ik meer details moet hebben. Vooraf moet je wel denken (of opschrijven) welke soort termnen in de volledige lagrangiaan moeten instaan.

Vraag 2: Begin met de bewegingsvergelijkingen voor een geladen deeltje

$(i{\gamma }^{\mu }{\partial }_{\mu }-e{\gamma }^{\mu }{A}_{\mu }-m)\psi =0$

Bewijs dat ${\psi }^c\equiv C{\overline{\psi }}^T$ voldoet aan $(i{\gamma }^{\mu }{\partial }_{\mu }+e{\gamma }^{\mu }{A}_{\mu }-m){\psi }^c=0$ Als C een matrix is met de eigenschap $C({\gamma }^{\mu }{)}^T{C}^{-1}=-{\gamma }^{\mu }$. Hints:

• bereken eerst de vergelijkingen voor $\overline{\psi }$ en transponeer deze.
• De expliciete representatie van de $\gamma$-matrices heb je niet nodig tot aan dit punt, maar het zou kunnen dat de formule $({\gamma }_{\mu }{)}^{†}={\gamma }^0{\gamma }_{\mu }{\gamma }^0$ handig is.

Toon dan aan dat $C=i{\gamma }^2{\gamma }^0$ een goede keuze is voor de $\gamma$-matrix representatie die in het formularium staat. ( Dus nu moet je die wel gebruiken.) Wat is met deze C een kortere formule voor ${\psi }^c$? (Zodanig dat je niet eerst $\overline{\psi }$ en dan de transpose moet berekenen) Neem nu voor en $\psi$ de toestand van een positron met spin down in rust. Toon dan aan dat ${\psi }^c$ dan een elektron is met spin up (en ook in rust). (We vermoeden dat deze opgave weleens fout zou kunnen zijn)

Vraag 3: Beschouw de koppeling van het elektron aan het Z-deeltje, vertrekkend van de mixing vertices die in het formularium staan ( en met $g^{\prime }=g_{W}tan{\theta }_W$). Bewijs dat de koppeling gegeven wordt door

$\frac{1}{2}{g}_Z\overline{e}{\gamma }_{\mu }(c_V-c_A{\gamma }_5)e$,

waar $g_Z=\frac{g_W}{cos{\theta }_W}=\frac{g^{\prime }}{sin{\theta }_w}$,

$c_V=-\frac{1}{2}+2si{n}^2{\theta }_W$

$c_A=-\frac{1}{2}$.

Hint: vereenvoudig snel al uw uitdrukkingen door te gebruiken dat je enkel bijdragen van het elektron en van het Z-deeltje nodig hebt. Wat zijn dan effectief de uitdrukkingen van de grootheden die in die vertices staan?

19 juni 2009

Deel 1 (Severijns):

Vraag 1: (mondeling)

Vergelijk de driftkamer met de Time Projection Chamber (TPC).

Vraag 2: (schriftelijk)

a: Via welk type verlopen volgende reacties, en waarom?

• ${\mathrm{\Sigma }}^{+}\to p{\pi }^0$
• $n^{\prime }\to {\pi }^0{\pi }^{0}n$
• $e^{-}{v}_{\mu }\to e^{-}{v}_{\mu }$

b: Koppel verval processen aan foto's van die processen in een detector.

Vraag 3: (schriftelijk)

Vergelijk het energie verlies door synchrotron straling van een electron met een proton in de LEP en LHC versnellers. (Alle formules en andere nodige gegevens zijn gegeven).

Vraag 4: (schriftelijk)

Geef de feynmann diagrammen van volgende reacties. Vermeld of ze leptonisch, semileptonisch of hardonisch zijn.

• ${\mu }^{-}{v}_e\to e^{-}{v}_{\mu }$
• $p{v}_{\mu }\to p{v}_{\mu }$
• ${\mathrm{\Delta }}^0\to p{\pi }^{-}$

Deel 2 (Van Proeyen):

Vraag 1: (Mondeling)

• Het standaard model wordt ook wel het model van SU(3)xSU(2)xU(1) genoemd. Leg uit.
• Bepaald dit model het aantal deeltjes van een soort, of welke wel en welke niet. Bepaald dit model de massa van de deeltjes?
• Hoe moet je het standaard model meer vastleggen?

Vraag 2: (schriftelijk)

• Toon aan dat ${\gamma }^0{S}^{+}{\gamma }^0=S^{-1}$ als S de lorentz transformatie matrix $S=a_{+}+a_{-}{\gamma }^0{\gamma }^1$ is. (met $a_{\pm }=\pm \sqrt{(\gamma \pm 1)/2}$)
• nog 2 deelvragen, maar die weet ik niet meer.

Vraag 3: (schriftelijk)

Quark antiquark verstrooiing waarbij een blauw antiquark en een rood quark verstrooid worden. Beschouw enkel de kleur factoren in het matrix element. Bereken de factor die daardoor in M komt.

23 juni 2008

Deel 1 (Van Proeyen):

Vraag 1:

Beschouw de overgang voor grote $M_W$ massa van het eerste diagram naar het tweede. Schrijf het eerste diagram volledig op. Negeer dan alle gamma matrices en factoren zoals 1/2, en schrijf op waarmee de tweede vertex zsou moeten evenredig zijn. Beschouw de dimensies van alle grootheden (met $\hslash$=c=1), en argumenteer dat dit leidt tot de matrix elementen van de juiste dimensie.

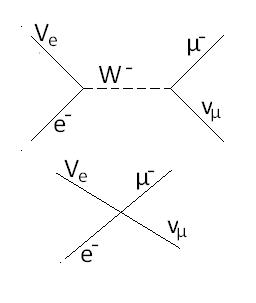
Vraag 2:

Verstrooiing van electron aan foton. Schrijf het laagste orde matrixelement neer en de som over polarisaties voor |${ℳ}{|}^2$. Het foton is geen on-shell fysisch deeltje. Je schrijft in het diagram voor het uitwendige foton een factor ${ϵ}^{\mu }$(p), maar laat dit als een vrije factor, waar je geen eigenschappen voor gebruikt. Wat zou er veranderen voor het up quark, wat voor het neutrino?

Vraag 3:

Leg uit wat het verschil is tussen de renormalisatie van de koppelingsconstanten van elektrodynamica en die van sterke interacties.

• Wat betekent 'renormalisatie'van de koppelingsconstanten? (omwille van welk probleem doen we dat? Waarom is het een oplossing van het probleem). Dit deel moet zeker niet langer zijn dan 10 lijntjes (of zelfs minder). Je moet geen formules gebruiken.
• Wat is het wiskundig verschillend gedrag? (2 lijntjes)
• Waarom zijn we gelukkig met dat verschil? (max. 8 lijnen tekst)

Deel 2 (Severijns):

Vraag 1:

Bespreek de violatie van pariteit bij de zwakke interactie.

Vraag 2:

Vergelijk de bubble-chamber met de nevelkamer (Wilson)

23 juni 2008

Er was geen deel van Severijns.

Deel 1 (Van Proeyen):

Vraag 1: Een infinitesimale Lorentz transformatie voor een spinor is ${\psi }^{\prime }=\psi +\frac{1}{4}{\gamma }^{\mu \nu }{\lambda }_{\mu \nu }\psi$, waar ${\lambda }_{\mu \nu }=-{\lambda }_{\nu \mu }$ de transformatieparameters zijn voor een transformatie van de vorm $x{\text{'}}^{\mu }=x^{\mu }+{\lambda }_{\nu }^{\mu }{x}^{\nu }$. Bewijs dat $\overline{\psi }{\gamma }^5{\gamma }^{\nu }\psi$ een pseudo-vector is. Je dient deze Lorentz transformaties te bezien, en ook de pariteitstransformatie, die op spinoren werkt als ${\psi }^{\prime }={\gamma }^0\psi$.

Vraag 2:

• Hoeveel Euler-Lagrange vergelijkingen zou je moeten neerschrijven voor een volledige Lagrangiaan van het standaard model? Dus je moet oplossen: wat zijn al de elementaire velden (tenminste het aantal van elke soort)? Welk zijn hun eigenschappen die bepalen hoeveel onafhankelijke reële functies deze bevatten?

• De ijksymmetrieën zijn relaties tussen deze vergelijkingen. Hoeveel relaties hebben we dan?

Vraag 3: Een rood quark wordt verstrooid aan een gluon van type 4 (van de $a^{\alpha }$ is enkel $a^4\ne 0$).

• Welk is de kleur van het uitgaand quark?
• Wat is de factor die je moet meenemen voor deze vertex en uitwendige factoren voor de quarks in het matrixelement.
• Werk de kleurfactoren uit.
• Als die twee quarks inkomende en uitgaande deeltjes zijn, waarom moet het gluon dan een virtueel deeltje zijn (je kan het Lorentz-frame beschouwen waar het eerste quark in rust is).

12 juni 2008

Deel 1 (Severijns):

Vraag 1: Leg uit waarom deeltjes-vervalprocessen waarbij S (strangeness) verandert mogelijk zijn

Vraag 2: Vergelijk de werking van een multi-wire chamber en een driftkamer

Deel 2 (Van Proeyen):

Vraag 1: In de Golden Rule komen integralen voor over elk deeltje van de vorm $\frac{d^3\overrightarrow{p_2}}{(2\pi {)}^{3}2E_2}$. Argumenteer waarom dit een vorm is die verenigbaar is met de Lorentz-transformatie.

Vraag 2:

De vertices die fotonen en Z-deeltjes koppelen aan fermionen worden gegeven in termen van de elektromagnetische stroom en de stroom van de derde component van de isospin. Schrijf deze neer in termen van $Z_{\mu }$ en $A_{\mu }$ en in termen van $j_{\mu }^3$ en $j_{\mu }^{em}$.

Als $g_e$ gedefinieerd wordt als de coëfficient in de vertex (geladen deeltje - geladen deeltje - foton) tussen de stroom en het foton, $V=g_e{j}_{\mu }^{em}{A}^{\mu }$, wat leidt je daar dan uit af voor de koppelingsconstanten?

Hoe ziet een vertex eruit voor de koppeling van het Z-deeltje aan deze stromen?

Maak dit nu expliciet voor het neutrino en het elektron. De koppeling van het neutrino aan het Z-deeltje stellen we voor als $V=\frac{1}{2}{g}_z{\overline{\nu }}_L{\gamma }^{\mu }{\nu }_L{Z}_{\mu }$. Wat vind je dan voor de waarde van g_z in termen van g_e en een hoek?

Zoek nu de koppeling van het elektron aan het Z-deeltje. De coëfficienten van koppelingen van fermionen $f$ aan het Z-deeltje worden geschreven als $\frac{1}{2}{g}_z{\gamma }^{\mu }(c_V^f-c_A^f{\gamma }^5)$. Voor het neutrino vinden we $c_V^f=c_A^f=\frac{1}{2}$, bereken deze getallen voor het elektron.

vraag 3:

Wat is de vertex voor een up-quark dat koppelt aan een foton?

12 juni 2008

Deel 1 (Severijns):

Vraag 1: (mondeling)

Leg uit hoe men is gekomen tot de onderstelling dat er elektron-neutrino's en muon-neutrino's bestaan, en hoe werd aangetoond dat dit inderdaad twee verschillende deeltjes zijn.

Bijvragen:

• hoe krijg je zo een bundel van alleen muon-neutrino's
• hoe noemt men de reactie muon + p -> n + muonneutrino (=muon-capture)
• ...

Vraag 2: (schriftelijk)

Leg uit hoe een Cerenkov detector werkt en hoe hiermee deeltjes met een welbepaalde snelheid kunnen geselecteerd worden.

Deel 2 (Van Proeyen):

Alles mondeling.

Vraag 1:

Wat zijn de waarden van ${\overrightarrow{j}}_{\mu }$ en $j_{\mu }^{e.m.}$ voor het up en down quark? Bv. je kan een antwoord schrijven van de vorm: $j_{\mu }^1=\overline{u}{\gamma }_{\mu }{\gamma }_{5}d$ ..., waar u en d staan voor de spinors van het up en down (maar dit is alvast een fout antwoord voor j_1).

Vraag 2:

Beschouw het verval van een W- deeltje in electron en (anti)neutrino.

1) Schrijf het matrixelement neer op laagste orde (geen lussen in het Feynman diagram).

2) Beschouw nu dat het W deeltje in rust vervalt, en maak een redelijke benadering als er sommen zoals $|E|+m$ komen met m de massa van het electron. Vergeet alle factoren die getallen zijn (2, pi, of gamma matrices) en schrijf op waarmee de levensduur evenredig is. Welke functie van de energie krijg je?

[Antwoord: je krijgt $\tau$ evenredig met $1/M_W$]

3) Bekijk opnieuw in al uw vorige berekeningen of de dimensies consistent zijn met wat we algemeen gezien hebben. Wat is de dimensie van elk object in de formules?

[Dit komt erop neer dat hij u bij wijze van spreke een hoop dingen aanduid en vraagt in welke eenheden die staan (hier: g_W, M (matrixelement van (1)), Gamma, tau, ...)

Vraag 3:

Tel de (reële) vrijheidsgraden van de bosonische deeltjes in het Weinberg-Salam model voor en na het Brout-Englert-Higgs mechanisme.

Oude examens

Niet meer zo relevant omdat het vak Deeltjesfysica toen gedoceerd werd door professor Gastmans en de huidige syllabus veranderd is tegenover toen.

29 juni 2007

Vraag 1

Bespreek de eigenschappen van volgende resonantie (dan tekening gegeven, het bleek om de ${\mathrm{\Delta }}^{++}$ te gaan)

Vraag 2

Bespreek K0 met CP behoud en bespreek die tijdsevolutie

Bijvragen

• Waarom is kleurlading bij quarks nodig? Hoe experimenteel gevonden?
• Hoe is het tau-lepton ontdekt? Hoe bereken je zijn levensduur?
• Hoe kan je experimenteel checken dat baryongetal behouden is?
• Wat is het CPT theorema, wanneer geldt het?

27 juni 2007

Opmerking: Dit examen werd ook gegeven op 28 juni in de voormiddag en in de namiddag, inclusief bijvragen

Vraag 1

$p+{\pi }^{-}\to n+{\pi }^0\to n+\gamma +\gamma$

Hoe kan je massa ${\pi }^0$ bepalen uit de min en max energie van fotonen?

Als $m_{{\pi }^0}$ = 135 MeV, wat is dan die maximale energie van de fotonen?

Vraag 2

Bespreek K0 met CP behoud en bespreek die tijdsevolutie.

Bijvragen

• Hoe weet je dat er meerdere soorten neutrino's zijn?
• Hoe is het tau-lepton ontdekt? Hoe bereken je zijn levensduur?
• Hoe kan je experimenteel checken dat baryongetal behouden is?
• Wat is het CPT theorema, wanneer geldt het?