Electroweak and Strong Interactions: verschil tussen versies
| Regel 11: | Regel 11: | ||
==De afgelopen examens== | ==De afgelopen examens== | ||
===27 May 2021=== | |||
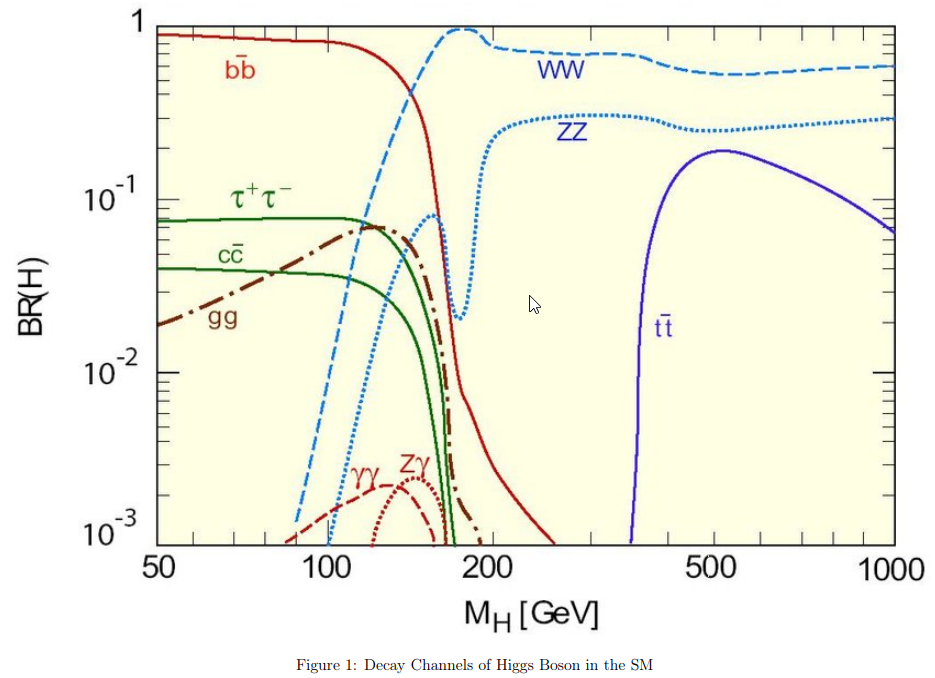
Consider the figure below: | |||
* Give a qualitative explanation for relative strength of the branching ratio to bb with respect to <math> \tau\tau </math> for low BEH masses | |||
* Give an explanation with Feynman diagrams of leading order decay of a scalar boson | |||
to a gluon-gluon pair and a photon-photon pair. | |||
* Define the concepts of partial decay width, total decay width and branching ratio of a decay process and explain the dip in the ZZ producing process branching ratio | |||
* Discuss the production of a WW and ZZ boson pair from the decay of scalar boson | |||
and explain when these modes are possible and give the respective decay process. Justify why the WW branching ratio is significantly higher than the ZZ branching ratio. | |||
[[Bestand:Decay channels higgs.png]] | |||
===28 juni 2019=== | ===28 juni 2019=== | ||
Versie van 27 mei 2021 14:01
Samenvattingen
Klik hier om de samenvattingen te bekijken
Algemene informatie
Dit is eigenlijk een vak van de VUB, maar dat wel vaak gevolgd wordt door Leuvense studenten. Dit is een vervolg op kwantumveldentheorie; ook gegeven door prof. Sevrin, en ook in dezelfde stijl. Dit jaar stonden er 5 punten op een taak die je moest maken tegen ergens in de blok, over een bepaald onderwerp dat we gezien hadden in de les (of niet), en dat uitspitten en wat in detail bespreken (5-10 blz).
Informatie over het examen
Het exaam bestond uit 2 vragen. Het "uiterst maximum" was 4,5 uur om ze op te lossen, maar uiteindelijk liep het mondeling e.d. uit tot een goeie 5-5,5 uur. Tegen dan zou je wel best iets hebben, anders zul je het wel niet zo goed gekund hebben...
Voor de rest: zie bij kwantumveldentheorie voor meer uitleg; dit vak en exaam is volledig analoog!
De afgelopen examens
27 May 2021
Consider the figure below:
- Give a qualitative explanation for relative strength of the branching ratio to bb with respect to for low BEH masses
- Give an explanation with Feynman diagrams of leading order decay of a scalar boson
to a gluon-gluon pair and a photon-photon pair.
- Define the concepts of partial decay width, total decay width and branching ratio of a decay process and explain the dip in the ZZ producing process branching ratio
- Discuss the production of a WW and ZZ boson pair from the decay of scalar boson
and explain when these modes are possible and give the respective decay process. Justify why the WW branching ratio is significantly higher than the ZZ branching ratio.
28 juni 2019
The exam had similar questions as the exams of the previous years. Professor Sevrin considered this as the easiest exam he made during this examination period, compared to the exams in Gent and Brussels and the other exam in Leuven.
Question 1
Consider a Higgs triplet
where the lagrangian density in the scalar sector is given by
and where transforms under the three dimensional representation of with the gauge transformation given by
The matrices obey the usual commutation relations and are given by
1) Discuss the groundstate(s) of the system.
2) Take as groundstate for the system
with . Determine the weak hypercharge such that the photon remains massless.
3) Give the Higgs multiplet in the unitairy gauge. An extra question on the oral part of the exam was to determine the electrical charge of the part of the the Higgs multiplet.
4) Determine the masses of the W and the Z gauge bosons.
5) Can you write down Yukawa couplings in this representation?
Question 2
We consider now the theory as it is used in the standard model and as we built it during the lectures. The coupling of the Brout-Englert-Higgs particle to the leptons and the quarks is given by
and the coupling to the W- and Z-bosons is given by
The fermion masses are given by
A plot of the braching ratios of the decay of the Higgs particle was given similar to that on the last page of the exam of 2011.
1) Compare the Higgs-fermion coupling strenght to the electromagnetic coupling strength of the fermions. Use .
2) Consider the and decay channels and explain.
3) Consider the and decay channels and explain. It is not necessary to explain the detailed form of the curves but a few Feynman diagrams would be nice.
4) Explain the form of the curves of the decay to WW and ZZ. The masses are approximately and . An extra question on the oral part was to explain why the branching ratio of the Higgs decaying to the W boson is bigger than the branching ratio of the decay to the Z-boson, since the later is heavier so one could expect the opposite situation.
31 May 2019
Very similar questions as the previous years. An extra question on the oral part was to explain why the branching ratio of the Higgs decaying to the W boson is bigger than the branching ratio of the decay to the Z-boson, since the later is heavier so one could expect the opposite situation.
8 juni 2015
Identiek hetzelfde examen als 11 juni 2012.
11 juni 2012
22 juni 2009
Vraag 1
Toepassing van het Higgs mechanisme.
Gegeven zijn twee scalaire velden en die als doubletten onder transformeren en beide hebben zwakke hyperlading . We gebruiken de notatie: met alle kes complexe getallen.
- Stel dat de vacuumsverwachtingswaarden van de scalaire velden door
en gegeven worden met v1 en v2 reeel. Wat zijn de massa's van de W, de Z, en het foton?
- Veronderstel dat de Lagrange dichtheid voor de scalairen door
gegeven is waar m1, m2 reeel en lamda_j>0 voor j in {1,2,3}. Bepaal v1 en v2 als functie van de diverse koppelingsconstantes.
- Bespreek de fysische vrijheidsgraden van de scalaire velden (maw geef een bondige analyse van de unitaire ijk). Toon bv aan dat het fysische elektrisch geladen veld door gegeven wordt met .
Vraag 2
Op zoek naar het Brout-Englert-Higgs deeltje. (een grote grafiek van de verschillende branching ratios is gegeven: [1], fig. 3 op p.8 - de figuur voor het exaam was ietsje anders, maar kwam op hetzelfde neer.)
De koppeling van het Higgs () aan leptonen of quarks () heeft de vorm en deze van de Higgs aan de W en Z velden Hierin worden de massa's gegeven door (alle massa's werden uitgedrukt in GeV/c^2 en komen van PDG)
- Op het volgend blad vind je de branching ratios voor het Higgs verval als functie van de Higgsmassa (). Geef een kwalitatieve bespreking van de bb, tautau, gammagamma, gg, WW en ZZ kanalen.