Toepassingen van Meetkunde in de Informatica

http://www.cs.kuleuven.ac.be/~dirkr/foto.jpg

oefeningen

oefening uit laatste oefenzitting

Laatste oefenzitting

http://static.flickr.com/70/152994638_00c7b383d1_m.jpg

http://static.flickr.com/74/152994136_19ebb442d2_m.jpg

http://static.flickr.com/52/152993572_347a6fb5af_m.jpg

Oefening op bepalen van het aantal snijpunten

Fout bij het aanmaken van de miniatuurafbeelding: Bestand is zoek

bepalen van alle snijpunten in een willekeurige verzameling lijnstukken (klik voor groter)

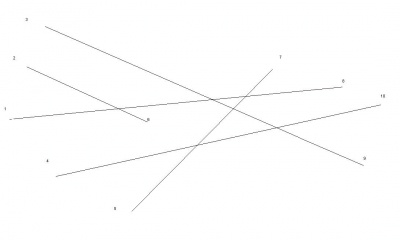
Gegeven: een willekeurige verzameling lijnstukken
Gevraagd: vind een algoritme dat ALLE snijpunten vindt
Oplossing: iemand?

examen

theorie

Bezier curven

• Bespreek C? continuiteit.
• hoe bekomt men C? continuiteit bij samengestelde bezier curven
• geef het algoritme van de Casteljau
• variatieverminderingseigenschap algemeen + wat betekent ze specifiek voor beziercurven
• bespreek subdivisie + methode
• bespreek graadverhoging + bewijs formule + nut
• waarom gebruikt men samengestelde beziercurven + wat voor problemen treden erbij op?
• bespreek constructie van samengestelde b?ziercurven + voor/nadelen
• tensor-product Bezier-veeltermen hoe?
• Afgeleide Dxy(x0,y0) in hoekpunten parameteropp. afleiden + grafisch weergeven.
• bespreek de constructie van tensor bezier product en leidt D(uv) af + grafische interpretatie

B-spline curven

bewijs dat de sommatie tot een eigenschap geldt voor de genormaliseerdeB-splines dwz voor u ? [un, um)

---

hoe kan men bij splines punten laten interpoleren door het samennemen van controlepunten? hoeveel moeten er samenvallen?

---

variatieverminderingseigenschap algemeen + wat betekent ze specifiek voor splines

---

algoritme van de boor + nauwkeurige tekening en bewijs van correctheid

---

hoe kan je ervoor zorgen dat een deel van een spline curve een recht lijnstuk is? waarom?

---

hoe spline interpoleren met meervoudige knooppunten.

algemeen

wat is bounding box quick rejection test uit algo om te bepalen of 2 rechten elkaar snijden geef de 2 toepassingen in het algo + implementatie

---

bespreek het algoritme voor het bepalen van de onderbrug en bovenbrug waarom is de kleinste y-coordinaat een slechte schatting voor het bepalen van de onderbrug?

---

geef een algoritme dat in O(N log N) bewerkingen nagaat of in een vz van N lijnstukken er snijdende lijnstukken in voorkomen Bewijs correctheid van dit algoritme geef beknopt hoe dit algoritme en de gegevensstrukturen moeten aangepast worden om alle snijdingen te vinden

---

geef een algoritme voor de berekening van het VPP van een vz van N punten in O(nlog n) bewerkingen verantwoord de rekencomplexiteit

---

bespreek graham scan + correctheidsbewijs + toon aan dat dit O(nlogn)bewerkingen gebeurt

---

wanneer is de inpakmethode (jarvis march) efficienter dan de methode van graham +(graham scan)

Voronoi diagrammen

bewijs: een voronoi diagramma van een vz S heft maximaal 2N - 5 voronoipunten en 3N - 6 voronoi zijden

---

een voronoiveelhoek van een punt pi is begrensd <=> pi element van inw(CH(S)) + nut + waar hebben we dit gebruikt?

---

bewijs dat minimale doorloopboom deelverzameling is van de Delaunay triangulatie wat is het nut van deze eigenschap?

---

2 dichtste buren hebben een gemeenschappelijke voronoizijde: bewijs

---

geef strategie + hoog-niveau algoritme voor het vinden van de maximale lege cirkel binnen de COV van een verzameling punten.

---

p(i) behoort tot de inwendige van V(i) asa V(i) is begrensd

nabijheidsproblemen

wat betekent volgende uitspraak: probleem A is ?(N) transformeerbaar tot probleem B? waarvoor kan een dergelijke uitspraak nuttig gebruikt worden + vb

---

wat is een EMDB van een vz punten + verband met Voronoi diagramma van een vz punten?

---

bespreek beknopt hoe een EMDB van een vz punten kan berkend worden in O(nlogn) bewerkingen

Fortune

bespreek de overganspunten bij fortune-algoritme

---

Bespreek de events in het algoritme van Fortune Welke acties moeten ondernomen worden?

---

hoe bepaal je het gebied dat kan bereikt worden door een robotarm met 3 links is de volgorde van de stukken belangrijk?

---

minkovski-som gebruiken en zeggen welke het is

oefeningen

vraag1

Gegeven een 3 link probleem L1 = 150 L2 = 75 L3 = 40 Los op voor een punt P dat op 180 cm van de schouder ligt.

vraag2

Maak een hoog-niveau algoritme voor alle snijdingen van een verzameling cirkels.

vraag3

een minkowski-som tekenen

vraag4

gegeven punten op cirkel. Vind de driehoek met het grootste oppervlak.
(opl mbv tegenvoetparen)

vraag5

bespreek of 2 eenvoudige veelhoeken geheel of gedeeltelijk overlappen (uitleg + hoog niveau algo)
in O((N + M) log (N + M)) bewerkingen

vraag6

1 punt gegeven en allemaal lijnstukken (niet snijdende) rond dat punt
schrijf algo om te controleren of je een rechte kunt tekenen vanuit het gegeven punt tot al die rechten
(maw: welke rechten zijn zichtbaar voor dat punt)

vraag7

gegeven een eenvoudige veelhoek
bepaal of pi, pi+2 een diagonaal is van die veelhoek in O(n)

vraag8

n cirkels, elk bepaald door middelpunt pi en straal ri
bedenk een strategie om na te gaan of er cirkels snijden + algo

vraag9

algoritme om na te gaan of pi,pi+1 diagonaal in eenvoudige veelhoek
is in O(n)