Differentiaalvergelijkingen

Inleiding

Qua studiepunten (8) is dit het zwaarste vak van het eerste semester van de tweede Bachelor. Er worden twee keer per week hoorzittingen gehouden, en er is één keer een oefenzitting. Dit is eigenlijk wat te weinig (cfr. Inleiding tot de Hogere Wiskunde, dat evenveel studiepunten heeft maar twee oefenzittingen had), waardoor het tempo bij de oefeningen erg hoog ligt. Ook wordt er een leidraad voor zelfstudie gegeven, dit is lesmateriaal uit de cursusnota's dat je zelfstandig moet verwerken maar waarvoor in de les de nodige theorie is gezien.

Het vak wordt gegeven door 3 professoren. Professor Van Assche geeft het deel over gewone differentiaalvergelijkingen (hoofdstukken 1-6). Professor Fannes geeft het deel over partiële differentiaalvergelijkingen (hoofdstukken 7-14). Professor Kuijlaars geeft de oefenzittingen aan de wiskundigen. Die voor de fysici worden door assistenten gegeven.

Hierbuiten is er gedurende het jaar nog een practicumwerkje met de computer (Latex). In 2005/2006 ging dit over de numerieke methodes, in 2006/2007 over conforme afbeeldingen en in 2007/2008 en 2008/2009 kreeg wiskunde een taak over de numerieke methodes en fysica over complexe integratie (2008-2009: de vergelijking van Laplace in 2D). Studenten van een andere bachelor mochten kiezen tussen beide.

Wina verdeelt de cursus, deze bevat ongeveer 240 bladzijden. Het eerste deel wordt algemeen als niet zo moeilijk beschouwd, terwijl het tweede deel (dat veel toepassingen uit de fysica behandelt) dan weer wel als moeilijk bestempeld wordt.

Het examen van 2008/2009 is een open boek examen: dit betekent dat je het handboek, de cursusnota's die op Toledo beschikbaar zijn, je eigen lesnota's en uitgewerkte oefeningen mag meebrengen naar het examen. De oefeningen worden schriftelijk verbeterd door de personen die de oefeningen hebben verzorgd. Het theoriegedeelte is mondeling bij de twee titularissen.

De punten verdeling is als volgt: 8 punten op de theorie, 6 punten op de oefeningen en 4 punten op het practicum. Ten slotte zijn er nog drie punten te verdienen als volgt: 1 punt met de huistaken en actieve inzet tijdens de oefenzitting in de loop van het semester. Als verder het resultaat op theorie (deel1), theorie (deel2) en oefeningen op het examen telkens op 20 wordt uitgeteld en je minder dan 5 punten te kort komt om op alle drie de onderdelen geslaagd te zijn, krijg je 2 punten; indien je minder dan 10 punten te kort komt dan krijg je 1 punt.

Examenvragen

Tweede zit 2008-2009, 19 augustus 2009, voormiddag

Theorie Van Assche

• Een differentiaalvergelijking. $x^2{y}^{″}+5x{y}^{\prime }+4y=0$
  • zoek een oplossing met behulp van machtreeksen
  • geef een tweede lineaire onafhankelijke oplossing (dit moest met ordereductie, maar de eerste vgl was heel eenvoudig, het stond niet bij op het examen dat het met ordereductie moest)
  • geef de Wronskiaan van de oplossingen. (Als bijvraag op het mondelinge gedeelte zelf moest je kunnen uitleggen wat je nu kon afleiden uit de Wronskiaan)

• Gegeven: twee stelsel van twee differentiaalvergelijkingen en drie verschillende faseportretten.
  • zoek de kritieke punten en bepaal de aard ervan en bepaal welk faseportret bij welk stelsel hoort
  • (op het mondelinge gedeelte moest je ook de faseportretten kunnen interpreteren en kunnen uitleggen wat voor populatie ze konden voorstellen)

Theorie Fannes

• $\frac{du}{dt}=\underset{0}{\overset{t}{\int }}dyu(y)\cdot l(t-y)$ en $u(0)=u_0$
  • Bepaal L(u) (Laplace dus, ik ken de mooie L niet...)
  • Los de vergelijking op indien $l(t)=l_0$
• opgave 12.1 i)

Oefeningen

• Bepaal $e^{At}$ met $A=\left[\begin{array}{ccc}1& 3& 4\\ 0& 1& 3\\ 0& 0& 2\end{array}\right]$
• Los het volgende stelsel op: $x^{\prime }=Ax+\left[\begin{array}{c}0\\ 0\\ 2e^{2T}\end{array}\right]$

• Het was een Sturm-Liouville probleem. Meer weet ik niet meer

Eerste zit 2008-2009, 23 januari 2009, voormiddag

PDF met het examen: Media:Examen_23_januari.pdf‎. Ook hier komen de vragen niet letterlijk overeen met die op het examen zelf, en ik kan ook niet garanderen dat de opgaven foutloos zijn.

Eerste zit 2008-2009, 20 januari 2009, voormiddag

Pdf: Media:DV_20_januari_2009.pdf‎ De verwoording is niet letterlijk maar ik heb zoveel mogelijk proberen te reconstrueren (Thomas).

Eerste zit 2008-2009, 12 januari 2009, namiddag

Ik kan niet met die wiki werken dus een snelle pdf gemaakt, als iemand de matrix nog heeft die ben ik kwijt. Overigens is bij de eerste vraag ook T groter dan 0. En dit is de matrix $\left[\begin{array}{ccc}5& -3& -2\\ 8& -5& -4\\ -4& 3& 3\end{array}\right]$ Media:DV_2008-2009_12_januari.pdf‎

Eerste zit 2008-2009, 12 januari 2009, voormiddag

Pdf: Media:ExamenDV2009.pdf

Ik heb de pdf gemaakt zoals de vragen op het examen gegeven worden. (Dus de aanwijzing bij de theorie van prof. Fannes was gegeven op het examen.) Verder maakte prof. Van Assche nog een mopje in het begin door de hint te geven bij zijn eerste theorievraag: "Ik zal meteen iedereen gelijkschakelen: lieveheersbeestjes eten bladluizen, niet omgekeerd."

Eerste zit 2007-2008, 22 januari 2008, voormiddag

Theorie Van Assche

• Katten, Vossen en Muizen leven samen in een systeem. Als de vossen afwezig zijn leven de Katten en Muizen in een Lotka-Volterramodel. Als de katten afwezig zijn, leven de Vossen en de muizen in een Lotka-Volterra model. Als de Muizen afwezig zijn leven de katten en de vossen in een Malthusmodel zonder interactie.
  • Schrijf de vergelijkingen van dit systeem
  • Wat is de aard en de stabiliteit van het kritieke punt (0,0,0)?
  • Zijn er nog andere kritieke punten. Wat kan je hierover zeggen?
• Gegeven: $x^2{y}^{(2)}-5x{y}^{\prime }+9y=0$
  • Wat is de aard van het punt 0
  • Geef 2 lineair onafhankelijke oplossingen

Theorie Fannes

• Gegeven $x^2{y}^{(2)}+x{y}^{\prime }+(x^2+n^2)y=0$ waar y continu is in 0. De oplossing van deze vergelijking is de Besselfunctie van de eerste soort van orde n. Men kiest ook vaak een normalisatie $y^{(n)}=\frac{1}{2^{n}n!}$.
  • Leidt af dat $J_n=\frac{1}{2\pi }\underset{-\pi }{\overset{\pi }{\int }}d\theta e^{-i(n\theta -xsin\theta )}$ analoog als in de cursus 12.3.1
  • Bewijs dat de functie genormaliseerd is, zodat $y^{(n)}=\frac{1}{2^{n}n!}$
  • Leidt nu de de Fourrierreeks af voor de uitdrukking $(x,\theta )\mapsto e^{ixsin\theta }$
• Gegeven $-\frac{1}{r}\frac{dR}{dr}-\frac{d^{2}R}{d{r}^2}+\frac{n^2}{r^2}R=\lambda R$
  • Bewijs dat dit een reguliere Sturm-Liouville operator is
  • Wat is het natuurlijk scalair product geassocieerd met deze operator
  • Bewijs dat bij dit scalair product de gegeven operator Hermitisch is.

Oefeningen

• Gegeven een stelsel van differentiaalvergelijkingen $x^{\prime }=x-y$ en $y^{\prime }=x^2-y$
  • Zoek de kritieke punten, Geef aard en stabiliteit
  • Maak een faseportret en wat is het gedrag op lange termijn?
• Beschouw de PDV: $u_t=a(u_{xx}+2u_x)$ met randvoorwaarden $u(x,t)=0$ voor $x=0$ en $u_x=0$ voor $x=1$.
  • Toon aan dat dit voldoet aan een Sturm-Liouville probleem. Gebruik scheiden van veranderlijken: stel u(x,t)=X(x)T(t) en toon aan dat de je zo het volgend stelsel komt: $T+\lambda T=0$ en $a(\frac{d^{2}X}{d{X}^2}+2\frac{dX}{dx})+\lambda X=0$
  • Toon grafisch aan dat er oneindig veel eigenwaarden zijn.
  • Zoek de oplossing voor deze differentiaalvgl met beginvoorwaarde $u(x,0)=x$

Eerste zit 2007-2008, 21 januari 2008, namiddag

Theorie Van Assche

• Een stelsel oplossen met behulp van Jordanketens en hetzelfde stelsel ook oplossen met de $e^A$ methode.
• Twee slingers die verbonden zijn met een veer, stel de vergelijkingen op, hoe zet je dit om naar een eerste orde probleem en bespreek het kritieke punt (0,0,0,0) voor m_1=1, m_2=1, k=1, L=g.

Theorie Fannes

• Bepaal de divergentie van een vectorveld in poolcoördinaten met behulp van de Stelling van Gauss
• Los de Laplacevergelijking op en bereken de kern van het positieve halfvlak van ${\mathbb{ℝ}}^2$. Los de vergelijking wel op voor enkel oplossingen die gelijkmatig begrensd blijven.

Bijvraag: in de cursus staat het voor een cirkel, kan je dit hieruit afleiden? (antwoord: ja, kies uw middelpunt op (0,R) en laat dit naar oneindig gaan.)

Oefeningen

• Beschouw $x{y}^{(2)}-(3+x)y^{\prime }+2y=0$
  • geef de oplossing van de indiciële vergelijking
  • geef de recursie betrekking van de coëfficiënten van de oplossing mbv frobenius
  • geef de 2de lineair onafhankelijke oplossing
• Warmtevergelijking op een staafje, niet-homogeen ($\frac{\partial u}{\partial t}=c^2\frac{{\partial }^{2}u}{\partial x^2}-x$), bereken de stationaire oplossing, bereken de algemene oplossing.

Eerste zit 2007-2008, 15 januari 2008

Theorie Van Assche

• De twee veren (F ) zijn identieke harde veren. Het apparaat A zorgt voor een repulsief effect evenredig met de uitwijking.
  • Bepaal de kritieke punten en onderzoek de aard van de kritieke punten.
  • Wat is het verschil met de wet van Hooke.
• Beschouw het volgende stelsel van differentiaalvergelijkingen:

$\{\begin{array}{l}\frac{d{x}_1}{dt}=x_1+x_2-x_3\\ \frac{d{x}_2}{dt}=x_2-x_3+x_4\\ \frac{d{x}_3}{dt}=x_3+x_4\\ \frac{d{x}_4}{dt}=x_4\end{array}$.

• • Los het op met de eigenwaardemethode.
  • Los het op met de exponentiële van een matrix.

Theorie Fannes

• De vergelijking $\frac{\partial u}{\partial t}-c(\frac{{\partial }^{2}u}{\partial r^2}+\frac{1}{r}\frac{\partial u}{\partial r})=g$ moet opgesteld en opgelost worden. De situatie is een schijf met straal R; u is de hoeveelheid massa per oppervlakte-eenheid en g is de hoeveelheid oppervlakte per oppervlakte-eenheid en per tijdsheid. Men mag rotatiesymmetrie veronderstellen voor g en u, de beginvoorwaarde en de randvoorwaarde.
  • Leidt de continuïteitsvergelijking af, door een ring $R_1<r<R_2$ te beschouwen.
  • Geef de wet van Fick en gebruik deze om de bovenstaande vergelijking af te leiden.
  • Zoek de stationaire oplossing, als de randvoorwaarde u(R)=0 is.
• Je hebt twee concentrische cilinders met stralen $0<r_1<r_2$. Bereken de elektrische potentiaal $\mathrm{\Phi }$ die voldoet aan de Laplacevergelijking. Zodat $\mathrm{\Phi }(r_1)=0en\mathrm{\Phi }(r_2)=V$.

Oefeningen

• Beschouw $x{y}^{(2)}-(3+x)y^{\prime }+2y=0$
  • geef de oplossing van de indiciële vergelijking
  • geef de recursie betrekking van de coëfficiënten van de oplossing mbv frobenius
  • geef de 2de lineair onafhankelijke oplossing
• zij $x^{\prime }=P(x,y)$ en $y^{\prime }=Q(x,y)$ met Q en P hebben continu partiële afgeleiden.
  • toon aan dat indien $\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}>0$

er geen niet-constante periodieke functies als oplossingen zijn (hint: een niet-constante periodieke functie definieert een gesloten kromme in het xy-vlak, Pas de stelling van Green toe op een gepast vectorveld)

• • neem $P(x,y)=x-2y-x^3-x{y}^2,Q(x,y)=2x+y-x^{2}y-y^3$
    • de oorsprong is een evenwichtspunt; onderzoek de stabiliteit.
    • Laat zien dat er een niet constante periodieke functies(hint: ga over op poolcoördinaten)

Eerste zit 2007-2008, 15 januari 2008, reeks 2

Theorie Van Assche

• Drie communicerende vaten waarbij de hoeveelheid vloeistof behouden blijft (hier is tekeningetje en verhaaltje bij over bier). Dus 3 vaten, in elk 100 liter vloeistof, noem x1,x2,x3 de hoeveelheid alcohol in elk vat. Vat 1 is verbonden met 2, 2 met 3 en 3 met 1, elk geeft 10 liter vloeistof door. a) stel differentiaalvergelijkingen op voor dit systeem. b) Toon aan dat x1+x2+x3 constant is. c) stel bij begin: x1=1,x2=2 en x3 =1. Bespreek het gedrag van x1,x2 en x3 als $t\to \mathrm{\infty }$.
• In een tuin leven x(t) bladluizen en y(t) lieveheersbeestjes. In afwezigheid van insecticide volgen deze twee soorten een Lotka-Volterra model. Nu sproeien we insecticide in de tuin zodat een constant percentage c van beide soorten sterft (c<a, waar a de groeiparameter van de bladluizen is in het Lokta-Volterra model). Ste een systeem van DV op en bespreek de evolutie van beide soorten met en zonder insecticide.

Theorie Fannes

• De functie $J_1(x)$ is de oplossing van de vgl $x^2\frac{d^{2}y}{d{x}^2}+x\frac{dy}{dx}+(x^2-1)y=0$ die niet singulier is in nul met y'(0)=0.5 en y(0)=0. Stel $F(s)=\underset{0}{\overset{\mathrm{\infty }}{\int }}{J}_1(x)e^{-sx}dx$. Pas Laplacetransformatie toe op de vergelijking om een differentiaalvgl te vinden waar F aan voldoet (zoals in de cursus gedaan is voor $J_0(x)$). Toon aan dat $F^{\prime }(s)=\frac{C_1}{(s^2+1{)}^{\frac{3}{2}}}$.
• Los de warmevgl op op een tweedimensionale torus met een willekeurige beginvoorwaarde die "braaf genoeg" is. De punten op een torus worden geparametriseerd door twee hoeken ${\theta }_1$ en ${\theta }_2$ waarbij één hoek de hoek is die gemeten wordt "in de cirkel die de torus zelf is" en de andere de hoek is die gemeten wordt in de cirkel die de dwarsdoorsnede vormt. Aanwijzing: de laplaciaan op een torus is $\frac{{\partial }^2}{\partial {\theta }_1^2}+\frac{{\partial }^2}{\partial {\theta }_2^2}$

Oefeningen

• Gegeven de vgl $x^2\frac{d^{2}y}{d{x}^2}-7x\frac{dy}{dx}+16y=ln(x)$

a)Toon aan dat $y_1(x)=x^p$ met $p\in \mathbb{ℝ}$ een oplossing is van de homogene vgl. b) Neem y= y1 * u en stel zo een vergelijking op voor u. c) Geef de algemene oplossing voor y.

• 2de oefening gelijkaardig aan 13.6: Touwtje dat trillingen ondergaat. En y(0,t)=y(1,t)=0 (+ nog 2 beginvoorwaarden ??).

a) Leid eerst een stationaire oplossing phi(x) af. b) definieer u(x,t)=y(x,t)-phi(x). Leid de differentiaalvergelijking voor u af met bijhorende rand-/beginvoorwaarden. c) Bepaal de de algemene oplossing van y(x,t). d) Wanneer is y maximaal ?

Tweede zit 2006 - 2007, 29 augustus 2007

Theorie Van Assche

• Niet lineair stelsel: kritieke punten vinden, aard van kritieke punten onderzoeken, richtingsveld schetsen
• gegeven de Differentiaalvergelijking $x^2{y}^{(2)}(x)+x{y}^{\prime }(x)-(x^2+1)y(x)=0$
  • Zoek een machtreeksoplossing rond x=0
  • Hoe vind je een tweede lineair onafhankelijke oplossing?
  • Geef de eerste termen van die oplossing

Theorie Fannes

• Een bol met straal 1 wordt ondergedompeld in een temperatuursbad met temperatuur 1. de bol produceert een constante hoeveelheid warmte per volumeeenheid.
  • Geef de differrentiaalvergelijking die deze situatie beschrijft
  • Wat is een stationaire oplossing?
  • Hoe vind je in principe een algemene oplossing voor de differentiaalvergelijking. (niet uitwerken, gewoon zeggen hoe je het zou doen. Hoe vind je de homogene oplossing en welke particuliere oplossing gebruik je?)

• geef de Laplacetransformatie van de "zaagtandfunctie". (oef 7.2.37)

Oefeningen

• een deeltje beweegt op de x-as en $\frac{d^{2}x}{d{t}^2}=-\frac{1}{(1+x{)}^2}$
  • bewijs dat $E=\frac{1}{2}(\frac{dx}{dt}{)}^2-\frac{1}{1+x}$ een constante is voor de beweging
  • Toon aan dat als $x(0)=0$ en $x^{\prime }(0)>\sqrt{2}$ dat de limiet voor t oneindig oneindig is
  • los de vergelijking op voor $x(0)=0$ en $x^{\prime }(0)=\sqrt{2}$

• een trillende staaf met demping evenredig met de snelheid. geef de oplossing voor een gegeven beginvoorwaarde f(x). Dit was oefening 9.6.21 in den boek. Daar staat ook stap voor stap uitgelegd hoe je het moet oplossen. Die hints werden ophet examen niet gegeven...

Tweede zit 2006 - 2007, 20 augustus 2007

Theorie Van Assche

• In het bos van Heverlee leven x(t) fazanten volgens een logistiek bevolkingsmodel. Omwille van de jacht verdwijnen er per jaar h fazanten.
  • Stel de vergelijking op die dit systeem beschrijven en leg uit
  • Onderzoek het gedrag van de vergelijking voor $x(t)\mapsto \mathrm{\infty }$ zonder de vergelijking op te lossen. Je mag aannemen dat h voldoende klein blijft. Bijvraag: teken dit in een faseportret
  • Stel nu dat h toeneemt, wat is de kritieke waarde, en wat gebeurd er als h die overstijgt?

• Gegeven een stelsel: $\{\begin{array}{l}x(t)=5x(t)-y(t)\\ y^{\prime }(t)=x(t)+3y(t)\end{array}$
  • Los dit stelsel op met behulp van de methode van de eigenwaardes. Leg ook uit hoe deze methode werkt
  • Vorm dit stelsel om tot een tweedegraadsvergelijking en los het op.
  • Bespreek en vergelijk de uitkomsten

Theorie Fannes

• Een oneindig lange, radioactieve cilinder wordt uit een reactor gehaald. Daarna wordt hij in een ijsbad van 0 graden gedompeld, zodat de wanden ermee in goed geleidend contact staan. Omwille van de radioactiviteit wordt er per volume-eenheid een constante hoeveelheid warmte opgewekt. Neem aan dat het probleem onafhankelijk is van de z-coordinaat, zodat we in essentie een 2D probleem hebben
  • Geef de vergelijking die dit systeem beschrijft en leg uit.
  • Wat is de evenwichtssituatie?
  • Hoe kan men in principe deze vergelijking oplossen?

• Sturm Liouville probleem: $-\frac{d^{2}f}{d{x}^2}+V(x)f=\lambda f$. Met f(0)=f(L)=0 (en alle voorwaardes voor continuiteit en afleidbaarheid voldaan). Neem het natuurlijke inproduct.
  • Bewijs dat <f,Lf> $\ge$ 0, en leidt hieruit af dat de eigenwaardes ook groter zijn dan of gelijk zijn aan nul
  • Bewijs dat <f,Lf> = 0 asa f=0, bewijs dat er alleen positieve eigenwaardes zijn
  • Stel we kiezen $V(x)=V_0\ge 0$, wat is de kleinst mogelijke eigenwaarde voor dit probleem?

Eerste zit 2006 - 2007, 3 februari 2007

Theorie Van Assche

• In het bos van Heverlee leven x konijnen, y vossen en z katten. In afwezigheid van konijnen leven vossen en katten volgens een Malthus-populatiemodel, zonder interactie. In afwezigheid van vossen leven konijnen en katten volgens een Lotka-Volterra-model, en in afwezigheid van katten leven konijnen en vossen eveneens volgens een Lotka-Volterra-model. Stel een systeem van differentiaalvergelijkingen op dat de evolutie van de populaties vossen, katten en konijnen beschrijft. Het punt (0, 0, 0) is een kritiek punt van dit systeem: wat is de aard van dit kritieke punt? Bepaal alle andere kritieke punten. Wat kan je over deze andere kritieke punten vertellen?

• Bekijk de differentiaalvergelijking $y^{(3)}-(x+1)y^{\prime }+xy=0$. Een oplossing van deze differentiaalvergelijking wordt gegeven door $y_1(x)=\exp (x)$. Leid een tweede orde differentiaalvergelijking af waarmee twee andere oplossingen $y_2,y_3$ van de gegeven differentiaalvergelijking kunnen worden bepaald (lineair onafhankelijk van de gegeven oplossing). Hoe los je deze tweede orde differentiaalvergelijking op met behulp van machtreeksen? (Bijvraagje: wat is de convergentiestraal van de machtreeksoplossing die je bekomt?)

Theorie Fannes

• Twee kleine vraagjes over de gradiënt van een scalair veld:
  • Toon aan dat een gradientveld een conservatief vectorveld is (cfr. opgave in de cursus).
  • Hoe bepaal je de $\theta$-component van de gradiënt in bolcoördinaten? (cfr. opgave cursus)

• Zij $\mathrm{\Omega }$ een compact oppervlak in ${\mathbb{ℝ}}^d$. Zij S de klasse van scalaire velden s die voldoen aan de volgende eigenschappen: s is éénmaal continu differentieerbaar in $\mathrm{\Omega }$, de eerste en tweede afgeleiden van s kunnen continu worden uitgebreid tot op de rand van $\mathrm{\Omega }$, en s wordt nul op $\partial \mathrm{\Omega }$. Definieer $⟨u,v⟩=\underset{\mathrm{\Omega }}{\int }\overline{u}vdV$ voor alle functies u en v uit de klasse S. Toon aan dat $⟨\mathrm{\Delta }u,v⟩=⟨u,\mathrm{\Delta }v⟩$ voor alle u en v in S, en bewijs dat de eigenwaarden van de operator $\mathrm{\Delta }$ strikt positieve reële getallen zijn.

Eerste zit 2006 - 2007, 2 februari 2007

Theorie Van Assche

• Beschouw het volgende stelsel van differentiaalvergelijkingen: $\{\begin{array}{l}d{x}_1/dt=2x_1+x_2-x_3\\ d{x}_2/dt=2x_2+x_4\\ d{x}_3/dt=2x_3+x_4\\ d{x}_4/dt=2x_4\end{array}$. Bepaal de oplossing met behulp van de eigenwaarde methode, en ook met behulp van de matrix-exponentiële functie.
• Beschouw de differentiaalvergelijking $x{y}^{(3)}(x)+(2-x)y^{(2)}(x)-2(1+x)y^{\prime }(x)-4y(x)=0$. Twee oplossingen van deze vergelijking worden gegeven door $y_1(x)=\exp (-x)$ en $y_2(x)=\exp (2x)$. Zoek een differentiaalvergelijkingen van de tweede orde waaraan een derde oplossing $y_3$, lineair onafhankelijk van de vorige twee oplossingen, voldoet. Bestaat er een eerste orde differentiaalvergelijking waaraan $y_3$ voldoet?

Theorie Fannes

• Beschouw een dun staafje met lengte L waarvan de eindpunten op temperatuur 0 worden gehouden. De lokale temperatuur $u(x,t)$ voldoet aan $u_t-k{u}_{xx}=f(x,t)$, met $f(x,t)$ de warmte die "aangevoerd" wordt. Zij $u_0$ de beginverdeling van de temperatuur. Zoek de oplossing $u(x,t)$. Begin door $u$ te schrijven als $\sum _{n=1}^{\mathrm{\infty }}{c}_n(t)\sin \frac{n\pi x}{L}$.
• Middelwaardestelling voor harmonische functies in 3D...

Eerste zit 2006 - 2007, 30 januari 2007

Oefeningen

• Er zijn zieke dieren, gezonde dieren met korte immuniteit en gezonde dieren die vatbaar zijn voor ziekte.
  • x'=-axy+cz
  • y'=axy-by
  • z'=by-cz

1. Welke soort is x,y,z? Verklaar de termen
2. Laat zien dat x+y+z=N constant is.
3. Neem a=b=c=1 en N=9. Herleid dit stelsel tot een stelsel met 2 veranderlijken. Bepaal de evenwichten
4. Bepaal de stabiliteit van de evenwichten

• Golfvergelijkinge: 1D horizontale snaar met zwaartekracht.
  • $\frac{{\partial }^{2}u}{\partial t^2}=c^2\frac{{\partial }^{2}u}{\partial x^2}-g$
  • randvoorwaarden: u(0,t)=u(L,t)=0 t>0
  • beginvoorwaarden: u(x,0)=f(x), $\frac{\partial u}{\partial t}$ 0<x<L
  • Gebruik scheiding van veranderlijken

Eerste zit 2006 - 2007, 29 januari 2007

Theorie Van Assche

• Gegeven een linear stelsel. Er werd gevraagd de Wronskiaan te berekenen en hoe hij gebruikt kan worden om het stelsel op te lossen
• Er leven 3 soorten samen: eekhoorns, konijnen en vossen. In afwezigheid van vossen leven eekhoorns en konijnen samen in een logistiek model en in afwezigheid van eekhoorns (konijnen) leven de vossen en konijnen (eekhoorns) in een jager-prooi model. Stel de vergelijkingen op en onderzoek de aard van het kritieke punt (0,0,0)

Theorie Fannes

• Zij X een afbeelding gedefinieerd door $(Xf)(x):f(x)\mapsto -\frac{d^{2}f}{d{x}^2}$. Hierbij is f een functie die voldoet aan f(0)=f(L) en f'(0)=f'(L). We definiëren op deze klasse van functies een inproduct <f,g>=$\underset{0}{\overset{L}{\int }}\overline{f(x)}g(x)dx$.

1. Toon aan dat dit inproduct hermitisch is.
2. Toon aan dat X enkel reële eigenwaarden heeft. Bewijs verder dat eigenfuncties behorende bij twee verschillende eigenwaarden orthogonaal zijn.
3. Laat zien dat X enkel niet-negatieve eigenwaarden heeft.

• Warmtevergelijking in "3D". Beschouw de twee concentrische sferen, met respectieve stralen $R_1$ en $R_2$ waarbij $0<R_1<R_2$. Op het boloppervlak van de binnenste sfeer wordt de temperatuur constant 0 gehouden, en op de buitenste sfeer een constante temperatuur T. Op t=0 hangt de temperatuur enkel af van de voerstraal r.

1. Vertaal dit naar wiskundige vergelijkingen.
2. Bepaal een stationaire oplossing (voor $t\mapsto \mathrm{\infty }$).
3. Geef een algemene oplossing voor deze partiële differentiaalvergelijking.

Oefeningen

• Gegeven: xy" - (3+x)y' + 2y = 0. Geef de oplossingen van de indiciaalvergelijking, en een recursiebetrekking tussen de coëfficiënten. Geef dan twee lineair onafhankelijke Frobeniusreeksoplossingen.
• Beschouw een 1-dimensionale snaar met lengte L die voldoet aan $\frac{{\partial }^{2}u}{\partial t^2}=c^2\frac{{\partial }^{2}u}{\partial x^2}-2k\frac{\partial u}{\partial t}$. De randvoorwaarden zijn u(0,t)=u(L,t)=0. Veronderstel hierbij dat $0<k<\frac{c\pi }{L}$.

1. Geef de oplossingen met gescheiden veranderlijken, dus van de vorm u(x,t)=X(x)T(t).
2. Geef de algemene oplossing als de beginvoorwaarden u(x,0)=f(x) en $\frac{\partial u}{\partial t}(x,0)=0$ zijn.
3. Wat is de rol van de voorwaarde $0<k<\frac{c\pi }{L}$? Wat als $k>\frac{c\pi }{L}$?

Eerste zit 2005 - 2006, Fysica

Theorie Van Assche

• populatie herten voldoet aan logistiek model, maar ook jaarlijks h herten afgeschoten: geef dvgl, bespreek gedrag als t-> infinity (zonder uit te rekenen!) als h klein, wat als h groot (hint van mezelf: blz 94!)
• Een stelsel met 4x eigenwaarde 2, hoe vind je 4 lin onafh opl

Theorie Fannes

• Fourier van Cauchyverdeling met $k<0$
• Diffusievgl met rotatiesym: hoe zie je aan een bvw dat er een beperkt aantal deeltjes is? Leidt deze dvgl af: Iedereen heeft het met stelling van gauss gedaan, maar fannes is bij iedereen blijven doorvragen over een andere manier die meer fysisch was.

Oefeningen

• $x^{\prime }=y+ax(x^2+y^2)$ en $y^{\prime }=-x+ay(x^2+y^2)$: bewijs dat (0,0) enige krit punt is, leid dvgl voor $r=\sqrt{x^2+y^2}$ af, wat is de aard van het krit punt (afh van $a\in \mathbb{ℝ}$)
• $u_{tt}=c^2{u}_{xx}-2k{u}_t$ en $k>\frac{c\pi }{L}$ ($u_{tt}$ is tweede part afg van u naar t). Opl via scheiding veranderelijken met rvw: $u(0,t)=0$ en $u_t(L,t)=0$.
  Zoek dan alg opl als ook $u(x,0)=f(x)$ en $u_t(x,0)=0$
  Wat als $k>\frac{c\pi }{L}$?

Tweede zit 2005 - 2006, Fysica

Theorie Van Assche

• 
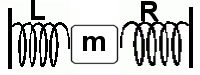
  • Bepaal de differentiaalvergelijking van dit systeem. Linkse veer is niet-lineair: $F(x)=-kx+a{x}^3$. Rechtse veer is lineair met veerconstante k.
  • Bepaal het gedrag van het systeem als $t\to \mathrm{\infty }$ en $a>0$.

(1 - x²)y"(x) + (1 - 3x)y'(x) + 3y(x) = 0

• Hoe vind je twee lineair onafhankelijke oplossingen?
  • Bepaal een eerste oplossing volledig (hint:veelterm)
  • Gebruik de eerste oplossing om een tweede te zoeken. Leg uit hoe.

Theorie Fannes

• Voor welke waarden van $a\in \mathbb{ℝ}$ is de matrix positief definiet?

Bereken voor dit geval de Fourriergetransformeerde van de functie $x\in {\mathbb{ℝ}}^2\to \exp (-x\cdot Rx)$.

• Diffusie binnen een bol van straal R in ${\mathbb{ℝ}}^3$. Begin- en randvoorwaarden zijn sferisch symmetrisch zodat de oplossing dezelfde sfeersymmetrie heeft. $u(x,t)=f(r,t)$ waar r de voerstraal is van het punt $x\in {\mathbb{ℝ}}^3$.
  • schrijf de PDF voor f
  • geef de rechtstreekse afleiding van de PDV (hint: 1. totaal aantal deeltjes 2. verandering: deeltjes door wand 3. deeltjesstroom radiaal 4. wet van Fick + elimineer deeltjesstroom)
  • $f(r,t)=g(r,t)/r$ geef PDV voor g
  • geef een maximale lineair onafhankelijke familie van oplossingen met gescheiden veranderlijken voor de randvoorwaarde .

Oefeningen

1. Populatie met gezonde, zieke en immune dieren voldoet aan volgend stelsel van DVs: $\{\begin{array}{l}{x}^{\prime }=-axy+cz\\ y^{\prime }=axy-by\\ z^{\prime }=by-cz\end{array}$ (dit komt er blijkbaar niet goed door?)
   1. Welke soort hoort bij welke variabele? Waarvoor staan de verschillende termen?
   2. Bewijs dat $x+y+z=N$ constant is.
   3. Stel $a=b=c=1,N=9$. Herschrijf naar systeem met 2 vergelijkingen en geef de evenwichtsposities.
   4. Geef de stabiliteiten van deze evenwichtsposities.
2. Snaar die langs de x-as loopt tussen $x=0$ en $x=L$. Op $x=b$ wordt ze uitgerekt met uitwijking $ϵ>0$. De resulterende beweging voldoet aan de golfvergelijking.
   1. Los op met scheiding van veranderlijken. Geef de oplossing als een reeksoplossing.
   2. Welke speciale reeks krijg je voor $u(x,t)$ met $t=0$ en $x=b=\beta L$?