Toepassingen van Meetkunde in de Informatica
| http://www.cs.kuleuven.ac.be/~dirkr/foto.jpg |
oefeningen
oefening uit laatste oefenzitting
| http://static.flickr.com/70/152994638_00c7b383d1_m.jpg | http://static.flickr.com/74/152994136_19ebb442d2_m.jpg | http://static.flickr.com/52/152993572_347a6fb5af_m.jpg |
Oefening op bepalen van het aantal snijpunten
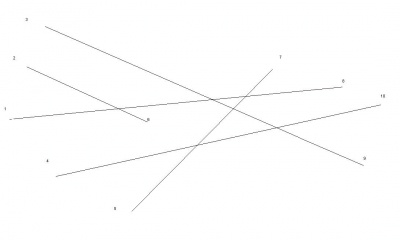
Gegeven: een willekeurige verzameling lijnstukken
Gevraagd: vind een algoritme dat ALLE snijpunten vindt
Oplossing: iemand?
examen
theorie
Bezier curven
- Bespreek C? continuiteit.
- hoe bekomt men C? continuiteit bij samengestelde bezier curven
- geef het algoritme van de Casteljau
- variatieverminderingseigenschap algemeen + wat betekent ze specifiek voor beziercurven
- bespreek subdivisie + methode
- bespreek graadverhoging + bewijs formule + nut
- waarom gebruikt men samengestelde beziercurven + wat voor problemen treden erbij op?
- bespreek constructie van samengestelde b?ziercurven + voor/nadelen
- tensor-product Bezier-veeltermen hoe?
- Afgeleide Dxy(x0,y0) in hoekpunten parameteropp. afleiden + grafisch weergeven.
- bespreek de constructie van tensor bezier product en leidt D(uv) af + grafische interpretatie
B-spline curven
- bewijs dat de sommatie tot een eigenschap geldt voor de genormaliseerdeB-splines dwz voor u ? [un, um)
- hoe kan men bij splines punten laten interpoleren door het samennemen van controlepunten? hoeveel moeten er samenvallen?
- variatieverminderingseigenschap algemeen + wat betekent ze specifiek voor splines
- algoritme van de boor + nauwkeurige tekening en bewijs van correctheid
- hoe kan je ervoor zorgen dat een deel van een spline curve een recht lijnstuk is? waarom?
- hoe spline interpoleren met meervoudige knooppunten.
algemeen
- Wat is bounding box quick rejection test uit algo om te bepalen of 2 rechten elkaar snijden. Geef de 2 toepassingen in het algo + implementatie
- bespreek het algoritme voor het bepalen van de onderbrug en bovenbrug waarom is de kleinste y-coordinaat een slechte schatting voor het bepalen van de onderbrug?
- geef een algoritme dat in O(N log N) bewerkingen nagaat of in een vz van N lijnstukken er snijdende lijnstukken in voorkomen
Bewijs correctheid van dit algoritme geef beknopt hoe dit algoritme en de gegevensstrukturen moeten aangepast worden om alle snijdingen te vinden
- geef een algoritme voor de berekening van het VPP van een vz van N punten in O(nlog n) bewerkingen
verantwoord de rekencomplexiteit
- bespreek graham scan + correctheidsbewijs + toon aan dat dit O(nlogn)bewerkingen gebeurt
- wanneer is de inpakmethode (jarvis march) efficienter dan de methode van graham (graham scan)
Voronoi diagrammen
- bewijs: een voronoi diagramma van een vz S heft maximaal 2N - 5 voronoipunten en 3N - 6 voronoi zijden
- een voronoiveelhoek van een punt pi is begrensd <=> pi element van inw(CH(S)) + nut + waar hebben we dit gebruikt?
- bewijs dat minimale doorloopboom deelverzameling is van de Delaunay triangulatie. wat is het nut van deze eigenschap?
- 2 dichtste buren hebben een gemeenschappelijke voronoizijde: bewijs
- geef strategie + hoog-niveau algoritme voor het vinden van de maximale lege cirkel binnen de COV van een verzameling punten.
- p(i) behoort tot de inwendige van V(i) asa V(i) is begrensd
nabijheidsproblemen
- wat betekent volgende uitspraak: probleem A is ?(N) transformeerbaar tot probleem B? waarvoor kan een dergelijke uitspraak nuttig gebruikt worden + vb
- wat is een EMDB van een vz punten + verband met Voronoi diagramma van een vz punten?
- bespreek beknopt hoe een EMDB van een vz punten kan berkend worden in O(nlogn) bewerkingen
Fortune
- bespreek de overganspunten bij fortune-algoritme
- Bespreek de events in het algoritme van Fortune Welke acties moeten ondernomen worden?
- hoe bepaal je het gebied dat kan bereikt worden door een robotarm met 3 links. Is de volgorde van de stukken belangrijk?
- minkovski-som gebruiken en zeggen welke het is
oefeningen
vraag1
Gegeven een 3 link probleem L1 = 150 L2 = 75 L3 = 40 Los op voor een punt P dat op 180 cm van de schouder ligt.
vraag2
Maak een hoog-niveau algoritme voor alle snijdingen van een verzameling cirkels.
vraag3
een minkowski-som tekenen
vraag4
gegeven punten op cirkel. Vind de driehoek met het grootste oppervlak.
(opl mbv tegenvoetparen)
vraag5
bespreek of 2 eenvoudige veelhoeken geheel of gedeeltelijk overlappen (uitleg + hoog niveau algo)
in O((N + M) log (N + M)) bewerkingen
vraag6
1 punt gegeven en allemaal lijnstukken (niet snijdende) rond dat punt
schrijf algo om te controleren of je een rechte kunt tekenen vanuit het gegeven punt tot al die rechten
(maw: welke rechten zijn zichtbaar voor dat punt)
vraag7
gegeven een eenvoudige veelhoek
bepaal of pi, pi+2 een diagonaal is van die veelhoek in O(n)
vraag8
n cirkels, elk bepaald door middelpunt pi en straal ri
bedenk een strategie om na te gaan of er cirkels snijden + algo
vraag9
algoritme om na te gaan of pi,pi+1 diagonaal in eenvoudige veelhoek
is in O(n)