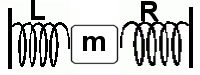Differentiaalvergelijkingen

Inleiding

Dit vak wordt gegeven door 3 professoren. Professor Van Assche geeft het deel over gewonen differentiaalvergelijkingen. Dit deel is niet echt moeilijk, zeker niet omdat het open boek is. Op het examen is hij de vriendelijkheid zelfe. Professor Fannes geeft het deel over partiële differentiaalvergelijkingen. Hiervoor gebruikt hij het boek en nog zo'n 100 pagina's eigen notities. Dit deel is iets lastiger en veel fysischer. Op het examen is porfessor Fannes iets norser dan zijn collega. Professor Kuijlaars geeft de oefenzittingen aan de wiskundigen. Die voor de fysici worden door assistenten gegeven. Het oefeningendeel op het examen is schriftelijk, er zijn op het examen geen nota's van de oefeningen toegelaten. Hierbuiten is er gedurende het jaar nog een practicumwerkje met de computer, voor de numerieke methodes.

De punten verdeling : 5 punten op het deel van Fannes, 5 op het deel van Van Assche, 6 op de oefeningen en 4 op het practicum.

Opmerking: Al deze gegevens kunnen nog wijzigen tegen volgend jaar!

Examenvragen

Eerste zit 2006 - 2007, Fysica

Theorie Van Assche

• Gegeven een linear stelsel. Er werd gevraagd de Wronskiaan te berekenen en hoe hij gebruikt kan worden om het stelsel op te lossen
• Er leven 3 soorten samen: eekhoorns, konijnen en vossen. In afwezigheid van vossen leven eekhoorns en konijnen samen in een logistiek model en in afwezigheid van eekhoorns (konijnen) leven de vossen en konijnen (eekhoorns) in een jager-prooi model. Stel de vergelijkingen op en onderzoek de aard van het kritieke punt (0,0,0)

Theorie Fannes

• Er werd een afbeelding X gedefinieerd: Xf(x)$\mapsto$-f"(x). Je moest aantonen dat het inproduct hermitsch was (het inproduct werd in een iets gewijzigde vorm gedefinieerd, in eindig interval, met periodieke RVW). Voorts moest je aantonen dat de eigenwaarden van de afbeelding reeel en niet negatief waren.
• Warmtevergelijking in "3D". Je had twee concentrische sferen, straal $R_1$ en $R_2$. De binnenste werd op constante temperatuur 0 gehouden, de buitenste op temperatuur T. Voorts hingen de beginvoorwaarden alleen af van de radiale afstand (de hoekafhankelijkheid viel dus weg, het werd in essentie 1D). Je moest dan de vergelijking opstellen, randvoorwaardes geven, $t\mapsto \mathrm{\infty }$ uitrekenen en tot slot de vergelijking oplossen.

De oefeningen

• Gegeven: $x{y}^{″}-(3+x)y^{\prime }+2y$ gevraagd naar de indiciaalvergelijking, recursiebetrekking en 2 lineair onafhankelijke oplossingen.
• Weet ik niet meer, iemand anders?

Eerste zit 2005 - 2006, Fysica

Theorie Van Assche

• populatie herten voldoet aan logistiek model, maar ook jaarlijks h herten afgeschoten: geef dvgl, bespreek gedrag als t-> infinity (zonder uit te rekenen!) als h klein, wat als h groot (hint van mezelf: blz 94!)
• Een stelsel met 4x eigenwaarde 2, hoe vind je 4 lin onafh opl

Theorie Fannes

• Fourier van Cauchyverdeling met $k<0$
• Diffusievgl met rotatiesym: hoe zie je aan een bvw dat er een beperkt aantal deeltjes is? Leidt deze dvgl af: Iedereen heeft het met stelling van gauss gedaan, maar fannes is bij iedereen blijven doorvragen over een andere manier die meer fysisch was.

Oefeningen

• $x^{\prime }=y+ax(x^2+y^2)$ en $y^{\prime }=-x+ay(x^2+y^2)$: bewijs dat (0,0) enige krit punt is, leidt dvgl voor $r=\sqrt{x^2+y^2}$ af, wat is de aard van het krit punt (afh van $a\in \mathbb{ℝ}$)
• $u_{tt}=c^2{u}_{xx}-2k{u}_t$ en $k>\frac{2\pi }{2L}$ ($u_{tt}$ is tweede part afg van u naar t). Opl via scheiding veranderelijken met rvw: $u(0,t)=0$ en $u_t(L,t)=0$.
  Zoek dan alg opl als ook $u(x,0)=f(x)$ en $u_t(x,0)=0$
  Wat als $k>\frac{c\pi }{2L}$?

Tweede zit 2005 - 2006, Fysica

Theorie Van Assche

Eerste vraag

• 1. Bepaal de differentiaalvergelijking van dit systeem. Linkse veer is niet-lineair: $F(x)=-kx+a{x}^3$. Rechtse veer is lineair met veerconstante k.
• 2. Bepaal het gedrag van het systeem als $t\to \mathrm{\infty }$ en $a>0$.

Tweede vraag

(1 - x²)y"(x) + (1 - 3x)y'(x) + 3y(x) = 0 Hoe vind je twee lineair onafhankelijke oplossingen?

• 1. Bepaal een eerste oplossing volledig (hint:veelterm)
• 2. Gebruik de eerste oplossing om een tweede te zoeken. Leg uit hoe.

Theorie Fannes

Eerste vraag

Voor welke waarden van $a\in \mathbb{ℝ}$ is de matrix positief definiet? Bereken voor dit geval de Fourriergetransformeerde van de functie $x\in {\mathbb{ℝ}}^2\to \exp (-x\cdot Rx)$.

Tweede vraag

Diffusie binnen een bol van straal R in ${\mathbb{ℝ}}^3$. Begin- en randvoorwaarden zijn sferisch symmetrisch zodat de oplossing dezelfde sfeersymmetrie heeft. $u(x,t)=f(r,t)$ waar r de voerstraal is van het punt $x\in {\mathbb{ℝ}}^3$.

• a) schrijf de PDF voor f
• b) geef de rechtstreekse afleiding van de PDV (hint: 1. totaal aantal deeltjes 2. verandering: deeltjes door wand 3. deeltjesstroom radiaal 4. wet van Fick + elimineer deeltjesstroom)
• c) $f(r,t)=g(r,t)/r$ geef PDV voor g
• d) geef een maximale lineair onafhankelijke familie van oplossingen met gescheiden veranderlijken voor de randvoorwaarde .

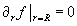Oefeningen

1. Populatie met gezonde, zieke en immune dieren voldoet aan volgend stelsel van DVs: $\{\begin{array}{l}{x}^{\prime }=-axy+cz\\ y^{\prime }=axy-by\\ z^{\prime }=by-cz\end{array}$ (dit komt er blijkbaar niet goed door?)
   1. Welke soort hoort bij welke variabele? Waarvoor staan de verschillende termen?
   2. Bewijs dat $x+y+z=N$ constant is.
   3. Stel $a=b=c=1,N=9$. Herschrijf naar systeem met 2 vergelijkingen en geef de evenwichtsposities.
   4. Geef de stabiliteiten van deze evenwichtsposities.
2. Snaar die langs de x-as loopt tussen $x=0$ en $x=L$. Op $x=b$ wordt ze uitgerekt met uitwijking $ϵ>0$. De resulterende beweging voldoet aan de golfvergelijking.
   1. Los op met scheiding van veranderlijken. Geef de oplossing als een reeksoplossing.
   2. Welke speciale reeks krijg je voor $u(x,t)$ met $t=0$ en $x=b=\beta L$?