Klassieke Mechanica

Inleiding

Dit vak heette tot 2005 Mechanica II. Het vak wordt gegeven door professor Janssen, net zoals het vak Algemene Natuurkunde I. Op het examen blijft professor Janssen doorvragen tot je ergens vast zit. Het is heel belangrijk dat je elk detail van de (vaak zeer wiskundige) afleidingen van buiten kent. Ook de oefeningen zijn niet zo eenvoudig. Dit vak mag dan ook zeker niet onderschat worden, wat nogmaals bleek uit het grote aantal buizen in eerste zit 2006. Waarschijnlijk zal de inhoud van het vak de komende jaren ook gemoderniseerd worden, onder andere door de invoer van een handboek dat nu nog niet beschikbaar was.

Examenvragen 2006

Januari 2006, eerste reeks

1. Leid de bewegingsvergelijkingen voor een probleem met centrale krachten af, meer bepaald de hereleiding tot een ééndimensionaal probleem
2. Leid de bewegingsvergelijkingen van Euler af.

Dan kwamen er nog twee oefeningen, één over een of andere eigenaardige slinger (ik snap het nog steeds niet echt eigenlijk), en één over rotatie rond een vaste as (die was vrij eenvoudig) --Stevie 9 jun 2006 13:03 (CEST)

Januari 2006, tweede reeks

Theorie

1. Bespreek vrije presessie (enkel tem hoeksnelheid van de presessie)
2. Pas variatierekening toe op de brachistochrone kromme (formule van variatierekenen moet niet afgeleid worden, maar is niet gegeven) en geef het principe van hamilton

Oefeningen

1. trein (m=10^5kg) rijdt met 100km/h naar zuiden, bereken zijdelingse kracht die trein op rails uitoefent als gevolg van draaiing aarde
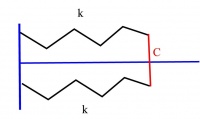
2. Staaf (lengte l, massa m) aan twee veren (één bovenaan, één onderaan; de veren hangen vast aan een muur), met massacentrum C dat op en rechte blijft, die loodrecht op de muur staat. Het systeem kan wel draaien en schuiven: bespreek mbv lagrange als de uitwijkingen klein zijn (zie afbeelding)

Fout bij het aanmaken van de miniatuurafbeelding: Bestand is zoek

Januari 2006, derde reeks

Theorie

1. Bespreek het verband tussen symmetrie en behoudswetten
2. Voer het begrip 'traagheidstensor' in. Hoe kan daarmee een uitdrukking opgeschreven worden voor het impulsmoment en de kin. energie van een star lichaam met een vast punt

Oefeningen

1. Een cilinder met massa m rolt zonder slippen recht naar beneden over een blok met dezelfde massa. Het blok heeft een hellingshoek alfa en het kan zelf zonder wrijving over het horizontale vlak glijden. Bereken, dmv Lagrange, de versnelling van het blok
2. Een kanon vuurt een projectiel af met een beginsnelheid van 500m/s onder een hoek van 45° met de horizontale. Het kanon vuurt in noordelijke richting en van op de grond, op een plaats met breedte graad 45°. Schat de zijwaartse versnelling van een dergelijk projectiel als het op de top van zijn baan is. Verwaarloos de luchtwrijving.

Januari 2006, vierde reeks

Theorie

1. Voer het begrip botsingsdoorsnede in, en leidt de formule van Rutherford af.
2. Leg aan de hand van een voorbeeld "normale trillingswijze" uit.

Oefeningen

1. Een dunne staaf met massa m is verbonden aan een vast punt. De staaf beweegt vrij in de ruimte onder invloed van de zwaartekracht (dus niet noodzakelijk in een vlak). Bespreek de beweging door middel van Lagrange.
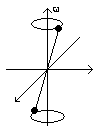
2. Een mathematische halter (twee puntmassa's verbonden door een massaloze staaf van lengte 2l) is in zijn zwaartepunt verbonden aan een vast punt. De halter draait rond de z-as (met constante hoeksnelheid omega) waarbij de halter een constante hoek alpha maakt met die z-as. (Zie tekening) Definieer een gepast relatief assenstelsel met de hoeken van Euler. Is er een krachtmoment nodig om de beweging te behouden?

Augustus 2006, eerste reeks

Theorie

1. Leidt de canonieke vergelijkingen van Hamilton af en geef de fysische betekenis van de Hamiltoniaan.
2. Gegeven zijn de beginposities en -snelheden van twee punten die verbonden zijn met een 1/r-potentiaal. Leidt de uitdrukking af voor de excentriciteit van de banen.

Oefeningen

1. Een mathematische slinger is verbonden aan het dak van een auto die met constante versnelling a beweegt. Stel de bewegingsvergelijking op met behulp van Lagrange door theta (de hoek tussen de vertikale en de slinger) als enige veralgemeende coördinaat (of als één van de veralgemeende coördinaten) te kiezen. Voor welke hoek is de slinger in evenwicht? Analyseer de beweging als de afwijking t.o.v. evenwicht klein is.
2. Prof G. Ekkemans wil in Leuven (54°N) zo snel bewegen dat de vertikale component van de Corioliskracht de zwaartekracht opheft. In welke richting moet hij dan bewegen om de snelheid zo laag mogelijk te houden? En hoe groot is dan die snelheid? Hoe groot is de horizontale component van de Coriolisversnelling dan?

Examenvragen 2007

Januari 2007, eerste reeks

Theorie

1. Bespreek de evenwichtspositie van een schietlood, rekening houdende met de draaiing van de aarde rond haar eigen as.
2. Bespreek de eendimensionale beweging van een punt op een as, voor posities rond het extremum van de potentiële energie. Hoe kan, bij een meerdimensionale beweging, de kinetische energie beschreven worden met behulp van de traagheidsmatrix.

Oefeningen

1. Een vouwladder bestaat uit twee benen die op een ideale gladde vloed staan. De benen hebben massa m en lengte l. De middens van de benen zijn verbonden door een ideale veer (natuurlijke lengte 0) met veerconstante k. Onderzoek de meest algemene beweging van het systeem. Kies hiervoor goede veralgemeende coördinaten en stel de bewegingsvergelijkingen van Lagrange op. Wat zijn de evenwichtsposities van het systeem? (Tips van de prof: De bewegingsvergelijkingen moeten niet opgelost worden. De ladder blijft wel met de voeten op de grond, en gaat dus niet vliegen.)
2. De hefkracht H, geleverd door de vleugels van een vliegtuig, staat altijd loodrecht op het vlak van het vliegtuig (dit is het vlak bepaald door de vleugels e de lengte-as). Stel dat een vliegtuig een horizontale snelheid van 880 hm/u heeft op een plaats op 55° breedtegraad. Bereken de hoek t.o.v. de lengte-as waarover de vleugels gedraaid moeten worden om de horizontale componente van de corioliskracht te compenseren.

Januari 2007, tweede reeks

Theorie

1. Leg het verband uit tussen symmetrie van een systeem en de behoudswetten van impuls, impulsmoment en energie.
2. Stel de bewegingsvergelijkingen van Euler op voor de beweging van een star lichaam met een vast punt. + geef voorbeeld waar deze gebruikt worden.

Oefeningen

1. Je hebt een staaf AB, met gegeven traagheidsmoment I, draait rond een punt op een verticale holle pikkel, beginsnelheid ${\omega }_0$. Er is een massa M die vrij en wrijvingsloos kan bewegen over de staaf. Deze is vastgemaakt aan een massaloos touwtje dat door de holle pikkel gaat en op het einde van dit draadje is een tweede massa m vastgemaakt. Deze tweede massa kan enkel verticaal bewegen. Stel de bewegingsvergelijkingen van Lagrange op. Kan het zijn dat de massa M ten opzichte van de staaf in rust blijft.
2. Een horizontale schijf draait rond een vertikale as door zijn middelpunt met constante hoeksnelheid. In het laboratorium laat men een massa m op een afstand R van het middelpunt los, waarbij men er zeer goed op let dat m in rust is ten opzichte van het laboratorium.
   1. Veronderstel dat er geen wrijving is tussen het punt en de schijf. Toon aan dat de massa m een cirkel beschrijft ten opzichte van de schijf. Leg het uit volledig bekeken vanuit het relatieve assenstelsel( Dus met schijnkrachten).
   2. Indien er wel wrijving is, zal de massa wegspiraliseren. Waarom?
   3. Hoe groot moet $\mu$ minimaal zijn opdat de massa nu in rust is tov de schijf en een cirkelbeweging maakt ten opzichte van het laboratorium.

Januari 2007, derde reeks

Theorie

1. Beschouw twee deeltjes die bewegen onder invloed van een onderlinge kracht, die steeds volgens de verbindingslijn gericht is. We hebben in de cursus een baanvergelijking voor afgeleid voor het equivalente eendeeltjesprobleem (zie formularium). Hoe kan je de excentriciteit e die voorkomt in deze vergelijking bepalen uit de beginvoorwaarden?
2. Precessie en nutatie...

Oefeningen

1. Lagrange-vergelijkingen, tekening nodig, zet ik er later wel eens op...
2. Op een vrachtwagen met een perfect glad "oppervlak" (laadruimte) ligt een perfecte cilinder, op afstand d van de rand van het oppervlak. De vrachtwagen en de cilinder zijn initieel in rust, en de vrachtwagen begint dan te rijden met een constante versnelling. Welke afstand heeft de vrachtwagen afgelegd op het moment dat de cilinder van de vrachtwagen valt?