Commutative Algebra

Samenvattingen

Klik hier om de samenvattingen te bekijken

Informatie over het examen

This master course is taught by Professor Smeets, as by 2019-2020. Professor Veys was the previous lecturer. Until the academic year 2012-2013 it was given in Dutch, with the name "modulen en homologische algebra" and a partly different content. Note that all true/false questions turned out to be true. Except in January of 2012, when there was an easy counterexample.

Examenvragen

Exam January 2025

Exam January 2025

Examen 16 januari 2023

Examenvragen

Examen januari 2020

The exam questions themselves are copyrighted. Below you can find a structure of the exam.

ORAL PART

One hour preparation time (at least). Three questions, for which some new creative input was required but which focussed mainly of variations/specific examples of course note theorems.

WRITTEN PART

Four hours time, minus the time you spent on the oral part. Four questions with several subquestions. All treat different chapters. Tempo is required and you should focus on the questions you can immediately answer, leaving the roadblocks for last. Solving the end-of-chapter exercises may net you an answer to a subquestion here-and-there.

Examen januari 2018

Er waren 3 theorie vragen waarvan er 1 mondeling uitgelegd moest worden. Bij de oefeningen gingen vraag 1 en 2 over de huistaken.

Oefening 3

Zij R en PID dat geen veld is. Classificeer alle eindig voortgebrachte projectieve , injectieve en platte modulen over R (dit waren dus eigenlijk drie vraagjes).

Oefening 4

Stel R = Z[t].

• Toon aan dat R / (2t-1) niet eindig voortgebracht is over Z.
• Zij f een veelterm in R. Toon aan dat R/(f) eindig voortgebracht is over Z als en slechts als f of -f monisch is.
• Zij I een ideaal in R. Toon aan dat R/I eindig voortgebracht is over Z als en slechts als I een monische veelterm bevat.
• Zij M een eindig voortgebrachte R-module. Stel dat R/rad(Ann(M)) eindig voortgebracht is over Z. Toon aan dat M eindig voortgebracht is over Z.

Exam January 2017

Exam January 2017

Exam January 15, 2013

The original file appeared on Toledo after the exams.

Examen januari 2012

Zowel de originele examenvragen als voorbeeldoplossingen verschenen dit jaar op Toledo.

Examen januari 2011

Media:ExamenModulen2011.pdf

Achteraf bleek dat oefening 4 verkeerd geformuleerd was, en werd deze vraag geschrapt.

Examen 12 januari 2010

Theorie

• Uitleg geven over de structuurstelling (stelling 3 op blz 35).
• Waar of niet waar: elke inverteerbare matrix over een euclidisch domein R is het product van elementaire matrices over R. Bewijs of geef een tegenvoorbeeld.
• Toon aan dat een pullback "uniek" is.
• De constructie van het morfisme ${\mathrm{\Delta }}_i$ uitleggen (blz stelling 5.3.2 van deel 3). Deze vraag was zonder voorbereiding.

Oefeningen

Opgave 1

Bewijs of geef een tegenvoorbeeld: Zij R een ring en M een module over R. Als M wordt voortgebracht door $m\in M$ en M is torsieloos, dan is M vrij.

Opgave 2

Berekening van een Jordanvorm en de rationale kanonieke vorm van een matrix.

Opgave 3

Definieer de categorie ${𝒞}$ als volgt: De objecten van ${𝒞}$ zijn eindige verzamelingen en de morfismen zijn bijecties hiertussen. Zij $X$ een object in ${𝒞}$. We noteren met $\mathrm{Sym}(X)$ de verzameling van permutaties van $X$ en met $Ord(X)$ de verzameling van orderelaties. Merk op dat je een orderelatie kunt noteren als $(x_{i_1}<\dots <x_{i_n})$ waarbij $n=\mathrm{\#}X$ en $x_i$ een opsomming is van de elementen van $X$

1. Definieer op logische wijze functoren, Ord en Sym, van ${𝒞}$ naar Set
2. Toon aan dat $Ord(X)\cong Sym(X)$ voor elke $X\in {𝒞}$
3. Toon aan dat er geen natuurlijke transformatie bestaat van Sym naar Ord (Hint: Beschouw $I{d}_X$ in $Ord(X)$ voor een zekere verzameling X en bekijk dan ${\eta }_X(I{d}_X)$).

Opgave 4

Zij R een ring. Definieer dan de ring $S=R\oplus R$. Beschouw het ideaal $I=\{(0,r)\mid r\in R\}$ van S. Toon aan dat I (gezien als S-module) projectief is maar niet vrij.

Opgave 5

Neem R een ring, M en N modulen over R. Neem een element $x\in R$ zodat x geen nuldeler is over M. Dit wil zeggen dat als $x.m=0$ dan m=0. Veronderstel ook dat x in de annihilator van N zit.

1. Toon aan dat Hom(N,M)=0.
2. Bewijs dat $Ex{t}^1(N,M)\cong Hom(N,\frac{M}{xM})$. Hint: gebruik het feit dat x geen nuldeler is en vertaal dit naar een korte exacte rij.

Examen 13 januari 2008

Theorie

• Bewijs van stelling 5 op pagina 29-32 van deel 1, met veel bijvragen. De eerste bijvraag was op voorhand gegeven: leg kort het basisidee van het bewijs uit.
• Bewijs dat een product van twee objecten in een willekeurige categorie 'uniek' is (en leg uit wat deze uniciteit betekent).
• Bewijs van stelling 5.5.2 ter plekke maken (zonder uniciteit, alleen het ketenmorfisme construeren). Je mag alleen het diagramma meebrengen. Uiteraard met een hele hoop bijvragen.
• Een extra (onvoorbereide) vraag over tensorproducten: met welke bekende ring is $\mathbb{ℝ}[x]{\otimes }_{\mathbb{ℝ}}\mathbb{ℂ}$ isomorf? En hoe zou je beginnen met dit te bewijzen

Oefeningen

Opgave 1

Waar of niet waar? Licht je antwoord toe:

• Zij k een veld. Een eindig voortgebrachte module over k[X] die een eindige dimensie heeft als vectorruimte over k is een torsiemodule. (Zoiets?)
• Laat R een ring zijn en $0\to N\to M\to N^{\prime }\to 0$ een kort exact rijtje. Als N en N' eindig voortgebracht worden, dan wordt ook M eindig voortgebracht.

Opgave 2

Zij A een abelse groep met voortbrengers $a_1,a_2,a_3$ en B een deelgroep voortgebracht door $4a_1+2a_2-2a_3$, $6a_1+4a_2+7a_3$ en $4a_1+2a_2+7a_3$. Schrijf in cyclische deelmodulen (primaire ontbinding) en geef de voortbrengers.

Opgave 3

Zij ${𝒞}$ een willekeurige categorie en zij $f,g:A\to B$ twee morfismen in die categorie. De gelijkmaker $k:K\to A$ van f en g is een morfisme zodat $f\circ k=g\circ k$ en voor elke andere gelijkmaker $m:M\to A$ bestaat er een uniek morfisme $l:M\to K$ zodat $k\circ l=m$.

• Toon aan dat de gelijkmaker een monomorfisme is.
• Wat is de gelijkmaker van f en g in de categorie van de Abelse groepen?
• Definieer de duale notie 'cogelijkmaker' in een willekeurige categorie.
• Wat is de cogelijkmaker van f en g in de categorie van de Abelse groepen?

Opgave 4

Zij R een ring. Beschouw het volgende diagramma, waarin de rijen exact zijn en $P_1,P_2$ projectief.

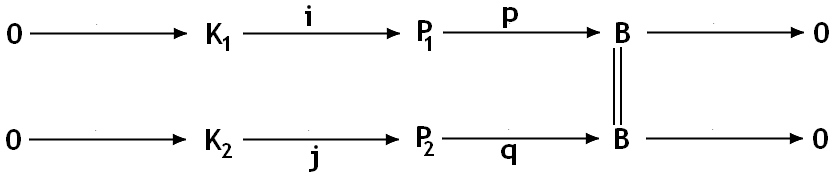
• Toon aan dat er een homomorfisme $\beta :P_1\to P_2$ bestaat zodat $p=q\beta$
• Toon aan dat er een homomorfisme $\alpha :K_1\to K_2$ bestaat zodat $j\alpha =\beta i$
• Zij $\psi :P_1\oplus K_2\to P_2:(x,k)\mapsto \beta (x)-j(k)$. Toon aan dat $\ker \psi \cong K_1$
• Toon aan dat $P_1\oplus K_2\cong P_2\oplus K_1$

Examen 4 september 2008

Theorie

• Bewijs van stelling 2 op pagina 40 van deel 1, met een hoop bijvragen.
• Vanalles met nulmorfismen.
• Bewijs dat een functor met een linksadjuncte pullbacks bewaart.
• Een diagram chase ("the five lemma"), ter plaatse uit te voeren.

Oefeningen

Opgave 1

Waar of fout? Argumenteer.

• Een projectieve, eindig voortgebrachte module over $\mathbb{ℂ}[X]$ is vrij.
• De kern en het beeld van een R-module homomorfisme (met R een commutatieve ring) van een Noetherse R-module naar een willekeurige R-module zijn beide opnieuw Noetherse R-modulen.

Opgave 2

Zij $p$ een priemgetal. Elk rationaal getal $q$ kan uniek worden geschreven als $q=p^k\frac{a}{b}$, met $a,b$ geheel, onderling ondeelbaar en niet deelbaar door $p$. We schrijven $v_p(q)=k$. Stel ${\mathbb{\mathbb{Z}}}_{(p)}=\{x\in \mathbb{\mathbb{Q}}:v_p(x)\ge 0\}\cup \{0\}$.

• Bewijs dat ${\mathbb{\mathbb{Z}}}_{(p)}$ een deelring is van $\mathbb{\mathbb{Q}}$.
• Bewijs dat ${\mathbb{\mathbb{Z}}}_{(p)}$ een Euclidisch domein is t.o.v. $v_p$.
• Zij $M$ een eindig voortgebrachte ${\mathbb{\mathbb{Z}}}_{(p)}$-module. Bewijs dat er een $\ell$ bestaat zodat $p^{\ell }M$ een vrije ${\mathbb{\mathbb{Z}}}_{(p)}$-module is.

Opgave 3

Invariante factoren van $XI-C$, met $C$ een gegeven 3 x 3 - matrix, en Jordan normaalvorm van $C$.

Opgave 4

Een vreselijk lange en nogal moeilijke opgave over de link tussen nuldelers in een commutatieve ring en lange exacte cohomologierijen... Ik ben niet helemaal zeker dat ik alles juist formuleer maar ik doe mijn best. Zij $R$ een commutatieve ring en zij $x\in R$. In deze opgave zullen we $0$ bekijken als nuldeler (tegen alle conventies in).

• Bekijk het complex $K(x)$ gegeven door $0\to R\to R\to 0$ met niet-triviale afbeelding $R\to R:r\mapsto rx$. Bewijs dat $H^0(K(x))=0$ als en slechts als $x$ geen nuldeler is in $R$.
• Bekijk het complex $K(x,y)$ gegeven door $0\to R\to R\oplus R\to R\to 0$ met niet-triviale afbeeldingen $R\to R\oplus R:r\mapsto (ry,-rx)$ en $R\oplus R\to R:(s,t)\mapsto sx+ty$. Toon aan dat dit inderdaad een complex is en bewijs dat, als $x$ geen nuldeler is, $y$ geen nuldeler is in $R/xR$ als en slechts als $H^1(K(x,y))=0$.
• Zij $K(x)[1]$ het complex dat je bekomt door $K(x)$ één plaats naar rechts te verschuiven. Bewijs dat er een exacte rij $0\to K(x)[1]\to K(x,y)\to K(x)\to 0$ bestaat van complexen, bepaal de geassocieerde lange cohomologierij van je exacte rij en bereken expliciet de connecterende homomorfismen.
• Stel nu dat $R$ een lokale ring is met maximaal ideaal ${ℳ}$. Stel dat $y\in {ℳ}$ en dat $H^1(K(x,y))=0$. Bewijs dan dat $x$ geen nuldeler is in $R$. Je kan hiervoor het lemma van Nakayama gebruiken.