Algebra I

Fout bij het aanmaken van de miniatuurafbeelding: Bestand is zoek

Fout bij het aanmaken van de miniatuurafbeelding: Bestand is zoek

Didactisch Team

Academiejaar	Professor(en)	Assistent(en)
2019-2020	Willem Veys
2020-2021	Professor 1(, Professor 2, ...)	Assistent 1(, Assistent 2, ...)

Samenvattingen

Klik hier om de samenvattingen te bekijken

- Notities van Syd

Inleiding

Algebra I is een vak ter waarde van 6 studiepunten, gegeven door professor Veys. De cursus bestaat uit ongeveer 180 bladzijden theorie en een aparte oefeningenbundel van ongeveer 20 bladzijden, beide verkrijgbaar bij Wina.

De leerstof is onder te verdelen in 4 stukken: groepen, ringen, velden en lineaire algebra.

Het examen bestaat uit 3 theorievragen en 4 oefeningen. De theorie is gesloten boek. De vragen komen letterlijk uit de cursus en twee ervan moeten later mondeling uitgelegd worden. Hij leest wel eerst je antwoorden, dus het is wel degelijk nodig dat je alles nauwkeurig uitschrijft. De derde theorievraag is enkel schriftelijk. Als je je theorie hebt afgegeven (na 1,5 uur ofzo), mag je je cursus bovenhalen en aan de oefeningen beginnen. Deze zijn puur schriftelijk. Je kan dus voor het mondeling nog eens in je cursus kijken naar de bewijzen.

Als je mondeling gedaan is stelt hij typisch nog wat "snelheidsvraagjes" om je inzicht te testen. Daarna mag je verder doen aan de oefeningen.

Je krijgt alles bij elkaar 5 uur tijd.

update 2024: Het examen duurt 4 uur, maar zonder een mondeling gedeelte. Er zijn nog altijd 2 tot 3 theorievragen (gesloten boek) en 4 oefeningen (open boek).

Handig om deze vakken gevolgd te hebben:

Lineaire Algebra & Algebraïsche structuren

Alle examens samen

Hier vind je alle examens Algebra I van deze examenwiki en andere examens Algebra I (soms ietwat andere syllabus) uit Gent en Antwerpen.

Examenvragen

Academiejaar 2024-2025

13 januari 2025

13 januari 2025

Academiejaar 2023-2024

30 augustus 2024

30 augustus 2024

15 januari 2024

15 januari 2024

Academiejaar 2022-2023

16 januari 2023

16 januari 2023

Opmerking: Vraag 2.3 is waarschijnlijk fout overgetypt ofzo, want R is helemaal geen veld, je kan nagaan dat X-2 een nuldeler is.

Academiejaar 2021-2022

17 januari 2022

17 januari 2022

29 augustus 2022

29 augustus 2022

Academiejaar 2020-2021

22 januari 2021

22 januari 2021

28 januari 2021

28 januari 2021

Academiejaar 2019-2020

28 augustus 2020

28 augustus 2020

Opmerking: de voorwaarde bij vraag 2.1 dat H eindig is kan niet kloppen, aangezien de te bewijzen puntjes niet juist zouden zijn. Een betere voorwaarde is dat H een eindige index heeft.

20 januari 2020

20 januari 2020

Verbetering: de eerste theorievraag gaat natuurlijk enkel over eindige commutatieve groepen (het is dus Propositie 1.6.2)

13 januari 2020

13 januari 2020

Academiejaar 2016-2017

19 januari 2017

19 januari 2017

• Opmerking: de allerlaatste matrix klopt niet, het element in de 3de kolom 5de rij moet 1 ipv -1 zijn en het element in de 3de kolom 6de rij moet -5 ipv 5 zijn.

Academiejaar 2015-2016

Theorie

• 1) a. Zij $H,K$ deelgroepen van een groep $G$. Dan is $HK=KH$ als en slechts als $HK$ een deelgroep is. b. Wat is de sterkste voorwaarde: $K$ is een normale deelgroep of $KG=GK$? verklaar.
• 2) Zij $R$ een commutatieve ring met eenheid. Bewijs dat een ideaal $I$ priem is als en slechts als $R/I$ een integriteitsdomein is.
• 3) Bewijs dat elk veld $K$ een uitbreiding $K_1$ heeft zodat elke veelterm in $K[x]$ een wortel heeft in $K_1$
• mondelinge bijvragen: wat als $I$ maximaal is in vraag 2? Zijn maximale idealen priemidealen in de gehele getallen? in het algemeen? Geef een toepassing op algebra die we hebben gezien in de les (bv cryptografie, het discrete logaritme probleem)?

Oefeningen

• • zij $G$ een $p$-groep en zij $N\subseteq G$ een normale deelgroep van orde $p$. Bewijs dat $N$ in het centrum van $G$ is bevat als en slechts als $N$ een normaaldeler is van $G$. (hint: bekijk conjugatieklassen van de elementen van N)
  • Zij $I,J$ twee idealen van een commutatieve ring met eenheid $R$ met $I+J=R$. Toon de chinese reststelling aan: $R/(I\cap J)\cong R/I\times R/J$. Gebruik dit om de klassieke chinese reststelling aan te tonen.
  • $F=\frac{\mathbb{\mathbb{Z}}[X,Y]}{5,X^2-Y,XY+X+1}$. Bewijs dat $F$ een veld is. Waarmee is $F$ isomorf? Heeft de veelterm $T^3+3T+2$ een wortel in het eindige veld van 125 elementen? Je moet geen expliciete wortel geven indien er één bestaat.
  • $\left(\begin{array}{ccccccc}-1& -1& 0& 0& -4& 0& 1\\ 0& -1& 1& -1& -4& 0& 2\\ 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& -1& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& -1& 1& 0\\ 0& 0& 1& 0& 0& 0& 1\end{array}\right)$, bepaal de jordanvorm en een bijhorende conjugatiematrix. [$(A-I{)}^{2}en(A+I{)}^3$ zijn gegeven]

27 augustus 2015

Herexamen 2015

15 januari 2015

Examen 15 Januari 2015

28 augustus 2012

Examen 28 augustus 2012

20 januari 2012

Examen 20 januari 2012

18 januari 2012

Theorie

• 1) Formuleer en bewijs de isomorfismestelling (=morfismestelling) voor groepen. (Schriftelijk)
• 2) Bewijs de stelling van Kronecker.
• 3) Waar of niet? Bewijs of geef een tegenvoorbeeld: "Als de ring $R$ een domein is, dan is ${\left(R\left[X\right]\right)}^{\times }=R^{\times }$."

Oefeningen

• 1) Gegeven is een groep $G$ met $102(=2\cdot 3\cdot 17)$ elementen, met $\left|Z\left(G\right)\right|=2$. Toon aan dat
  • a) $\left|Z(G/Z\left(G\right))\right|=1$
  • b) $G/Z\left(G\right)$ heeft een deelgroep van orde 17.
  • c) $G$ heeft een deelgroep van orde 34.

• 2) Stel dat R een HID is:

• • a) Bewijs dat een priemideaal van R een maximaal ideaal is.
  • b) Zij f een surjectief ringmorfisme van R naar S met S een integriteitsdomein. Bewijs dat ofwel f een isomorfisme is, ofwel S een veld.
  • c) Toon aan dat als de veeltermenring van R een HID is, dat R dan een veld moet zijn.

• 3) Zij p priem = 1 mod 3, beschouw Fp.

• • a) Toon aan dat er in $F{p}^x$ een element van orde 3 bestaat.
  • b) Besluit dat $X^2+X+1$ een wortel heeft in Fp

• 4)

The usual stuff: een 6x6 matrix die je naar Jordanvorm moet omwerken, je moest ook de minimale veelterm en de matrix van basisverandering kunnen geven.

21 januari 2011

Theorie

• schriftelijk
  • a) Zij G een groep en H een deelgroep van G van index 2. Toon aan dat H een normaaldeler is van G.
  • b) Zij G een groep, f:G->H een groepsmorfisme en N een normaaldeler van H. Toon aan dat $f^{-1}(N)$ een normaaldeler is van G

• mondeling
  • Zij R een ring. Toon aan dat de kandidaat-bewerking $.:\frac{R}{I}\times \frac{R}{I}\to \frac{R}{I}:(x+I).(y+I)\mapsto (x.y)+I$ goed gedefinieerd is als en slechts als I een ideaal is.

• schriftelijk
  • Zij V een eindigdimensionale vectorruimte en $A$ een element van $Hom(V,V)$. Bewijs in detail dat er een unieke $A^{*}$ bestaat zodat $⟨A(v),w⟩=⟨v,A^{*}(w)⟩$. Duid aan waar je gebruikt dat V eindigdimensionaal is. Je hoeft geen tegenvoorbeeld te geven als V oneindigdimensionaal is.

Oefeningen

• Oefening 1 :We bewijzen de eerste stelling van Sylow. Dit doen we in verschillende stappen. Doorheen deze oefening is p een priemgetal en G een groep.
  • Stel dat $p^k|\left|G\right|$ voor een $k\in {\mathbb{\mathbb{N}}}_0$. Toon aan dat er een strikte deelgroep H van G bestaat zodat $p^k|\left|H\right|$ of dat $p||Z(G)|$.
  • (Stelling van Gauss). Toon aan dat als $p|\left|G\right|$, dat er een element in G bestaat van orde p (Hint: toon dit eerst aan voor een commutatieve groep met de structuurstelling en dan in het algemeen)
  • (Eerste stelling van Sylow)Stel dat $p|\left|G\right|$ en zij k de grootste k waarvoor $p^k|\left|G\right|$. Dan heeft G een deelgroep S zodat $p^k=\left|S\right|$.

• Oefening 2:
  • Zij R een ring met eenheidselement en S een deelring zodat S 1 bevat. Beschouw nu de volgende equivalentie. R is een domein $⟺$ S is een domein. Een van deze implicaties is foutief, de andere is juist. Bewijs de juiste implicatie en geef een tegenvoorbeeld voor de foutieve.
  • Zij $F\subseteq K$ een algebraïsche velduitbreiding en zij R een ring zodat $F\subseteq R\subseteq K$. Toon aan dat R een veld is.
  • Geldt dit ook indien de uitbreiding niet algebraïsch is?

• Oefening 3: Zij F een veld en beschouw de veelterm f in F[X] gegeven door $X^7-11$. Zij E het ontbindingsveld van f over F. Geef de uitbreidingsgraad van E over F met $F=\mathbb{\mathbb{Q}},\mathbb{ℝ},\mathbb{ℂ}$ en ${\mathbb{𝔽}}_2$

• oefening 4: vind de Jordanvorm J van de matrix A. Bereken ook de minimale veelterm en de matrix P, zodat $A=P^{-1}JP$.

$A=\left(\begin{array}{ccccc}0& 0& 0& 0& 1\\ 2& 1& -1& -1& -1\\ 0& 0& 2& 1& 0\\ 0& 0& 0& 2& 0\\ -1& 0& 0& 0& 2\end{array}\right)$

19 januari 2011

Theorie

• Schriftelijk
  • a) Formuleer de eerste ismorfismestelling voor groepen.
  • b) Forumuleer en bewijs de parallellogramismorfismestelling voor ringen. Hint: Voor een ring R geeft deze stelling een verband tussen een ideaal I van R, een deelring S van R ,$I+S$ en $I\cap S$.

• Mondeling
  • Zij K een veld en G een eindige deelgroep van de multiplicatieve groep $K^X,\cdot$. Bewijs in detail dat G cyclisch is.

• Schriftelijk
  • a)Zij V een eindig dimensionale vectorruimte over een veld K en zij A een nilpotente transformatie van V met index $k\ge 1$. Zij $v\in V$ gegeven met $A^{k-1}(v)\ne 0$. Bewijs dat $v,A(v),...,A^{k-1}(v)$ lineair onafhankelijk zijn.
  • b) Veronderstel bovendien dat k = dim V. Wat is dan de matrix A ten opzichte van de basis {$v,A(v),...,A^{k-1}(v)$}?

Oefeningen

• Toon aan dat ${{𝒮}}_4$ geen deelgroep heeft die isomorf is met de quaternionengroep.

• Stelling van Wedderburn (p 45) aantonen in verschillende stappen. Zij R een eindig lichaam.
  • a) Zij $x\in R$. Definieer de ringcentralisator als $C_R(x)=\{r\in R|rx=xr\}$. Toon aan dat $C_R(x)$ een deellichaam is van R.
  • b) Definieer ringcentrum Z(R) van R als volgt: $Z(R)={\cap }_{x\in R}{C}_R(x)=\{r\in R|rx=xr$ voor alle $x\in R\}$. Stel dat |Z(R)| =q (vermits $0\ne 1$ in R en deze elementen beide behoren tot Z(R) hebben we dat $q\ge 2$). Toon aan dat er een $n\in {\mathbb{\mathbb{N}}}_0$ zodat $|R|=q^n$ en dat voor alle $x\in R$ een $n_x$ bestaat zodat $|C_R(x)|=q^{n_x}$.
  • c) Veronderstel dat R geen veld is, i.e. er bestaat een $x\in R$ zodat $C_R(x)\ne R$. Leg uit waarom n > 1 en $n_x<n$. Toon aan: $q^n-1=q-1+\sum _{k=1}^m\frac{q^n-1}{q^{n_k}-1}$ voor $m\in {\mathbb{\mathbb{N}}}_0$ met elke $n_k<n$ en $\frac{q^n-1}{q^{n_k}-1}\in \mathbb{\mathbb{Z}}$ voor elke k.
  • d) Dan kan men makkelijk aantonen dat $n_k|n$ (dat hoef je hier niet te doen). Maak hiervan gebruik om aan te tonen dat ${\mathrm{\Phi }}_n(q)|q-1$ (in $\mathbb{\mathbb{Z}}$), waarbij ${\mathrm{\Phi }}_n$ de n-de cyclotome veelterm noteert.
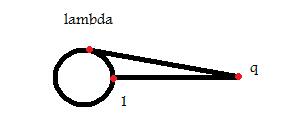
  • e) Uit onderstaande tekening haal je direct dat $|q-\lambda |>|q-1|$ als ${\lambda }^n=1$ en $\lambda \ne 1$. Maak gebruik van dit resultaatje om een contradictie uit te komen.

• Beschouw de ring $\frac{{\mathbb{\mathbb{Z}}}_2[X]}{X^2+1}$. Deze ring heeft 4 elementen. Is deze ring isomorf met ${\mathbb{\mathbb{Z}}}_2\oplus {\mathbb{\mathbb{Z}}}_2,{\mathbb{\mathbb{Z}}}_4,{\mathbb{𝔽}}_4$ of met geen van de drie? Leg uit.

• Zij $A\in M^{3\times 3}(\mathbb{ℂ})$ diagonaliseerbaar met 3 verschillende eigenwaarden ${\lambda }_1,{\lambda }_2$ en ${\lambda }_3$ en de bijhorende eigenvectoren $v_1,v_2$ en $v_3$. Beschouw de matrix $C\in M^{6\times 6}(\mathbb{ℂ})$ waarbij $C=\left(\begin{array}{cc}A& I\\ 0& A\end{array}\right)$.
  • a) Vind de Jordanvorm J van C.
  • b) Vind een matrix P zodat $P^{-1}CP=J$.

Januari 2010 Wiskunde

Examen 13 januari 2010

Tweede zit 02/09/09 Wiskunde/fysica

Theorie

• Zij $\sigma \in S_n,\sigma \ne Id$, geef en bewijs een formule voor de orde van $\sigma$ in termen van zijn disjuncte cykelnotatie.
• Zij R een ring en D een deelgroep van R,+ Bewijs dat

$\overline{\cdot }:R/D\times R/D\to R/D:(\overline{x},\overline{y})\to \overline{x\cdot y}$ goed gedefinieerd is als en slechts als D een ideaal is

• Bewijs ** De orde van een eindig veld is altijd een macht van een priemgetal.
  • Zij p een priemgetal en $r\in {\mathbb{\mathbb{N}}}_0$, dan bestaat er een veld met $p^r$ elementen, nl. het ontbindingsveld van de veelterm ... over ${\mathbb{\mathbb{Z}}}_p$

Oefeningen

• Zij G een groep, en D = { (g,g) | g element van G} deelgroep van G x G. Welke voorwaarde moet je op G opleggen zodat D een normaaldeler is? Stel nu dat D een normaaldeler is, waarmee is GxG / D isomorf?
• Een ring heet lokaal als de ring slechts 1 maximaal ideaal heeft. **Bewijs de volgende equivalentie: een ring is lokaal als en slechts als de niet-eenheden van de ring een ideaal vormen. **Zijn de volgende ringen lokaal: Z, Z_9, Z_10, Z_11 en Z[x].
• Zij $z=i\sqrt{1+\sqrt{2009}}$. Bereken [Q(z) : Q] en geef de minimale veelterm van z over $\mathbb{\mathbb{Q}}$.
• Zij $A\in {\mathbb{ℂ}}^5\times {\mathbb{ℂ}}^5$

$A=\left(\begin{array}{ccccc}1& 0& 0& 0& 0\\ 1& 2& -1& 1& 1\\ -2& 0& 3& -1& 0\\ -1& 0& 1& 1& 0\\ 0& 0& 0& 0& 2\end{array}\right)$ 

Bepaal een inverteerbare Jordanmatrix J zodat $J=P^{-1}AP$

Eerste zit 27/01/09, Wiskunde/Fysica

Media:ExamenAlgebraI2009.pdf

Snelheidsvraagje bij mij (Christophe): Geef alle idealen van Z. Z is een HID, is (4,7) dan ook een hoofdideaal? Wat is de priemdeelring van Z? Wat is de doorsnede van alle deelringen van Z? Wat zijn de maximale idealen in Z?

Eerste zit 21/01/09, Wiskunde

Theorie

• Bewijs de Stelling van Cayley: Elke groep is isomorf met een permutatiegroep
• Zij R een commutatieve ring met eenheidselement en I een ideaal van R. Bewijs: R/I is een veld asa I is maximaal. (Volledig Schriftelijk)
• Gegeven: Een veld K heeft een algebraïsche uitbreiding K1 zodat elke niet constante veelterm in K[X] een wortel heeft in K. Bewijs: Elk veld heeft een algebraïsche sluiting.

Oefeningen

• x en y zijn voortbrengers van de groep G. x^8 = y^2 = yxyx^3 = 1
  • Toon aan dat elk element van G van de vorm x^i y^j is. Toon aan dat elk element maximaal orde 16 heeft.
  • Zij |G|=16. Bepaal de orde van xy. Bepaal het centrum van G. Toon aan dat G oplosbaar is.
  • Toon aan dat elke groep van orde 4 dezelfde vorm als G heeft. Geldt ook voor elke groep van orde 8?
• Waar of vals, geef voldoende uitleg:
  • Zij R = IR^(2x2)(Dus reele matrices). Voor elke f,g uit R[X] geldt deg(f*g) = deg(f) + deg(g)
  • Zij R de directe som van S en T. Als R een eenheidselement heeft, hebben S en T ook een eenheidselement.
• • Hoeveel monische irreducibele veeltermen van graad 3 heeft Z_3[X].
  • Toon aan dat f(X) = X^2 + 2X + 1 irreducibel is. Wat is de orde van F = Z_3[X]/(f)?
  • Zij O = {ord(g)|g element van F^x}. Geef voor elke n element van O een element g uit F met deze orde.
• • Voor welke n bestaat er een matrix uit C^(n x n) zodat de minimale veelterm (x-1)(x-2)^2(x-3)^3
  • Zij A een nilpotente matrix van C^(6*6). Zij dim(ker(A^2))= 4. Geef alle mogelijke invariante systemen van A.

Eerste zit 28/01/08, Wiskunde

Theorie

• Formuleer en bewijs de tweede isomorfismestelling. (als je wou kon je de formulering van de stelling kopen voor 0,5 punten. Ze later aan andere mensen doorverkopen voor 0.25 punten was dan weer niet toegestaan.) - deze vraag was enkel schriftelijk, werd dus niet mondeling behandeld.
• Bewijs:
  • Het aantal elementen van een eindig veld is van de vorm $p^r$.
  • Er bestaat een veld met $p^r$ elementen, namelijk een ontbindingsveld van ... over ${\mathbb{\mathbb{Z}}}_p$.
• Bewijs dat diagonaliseerbaar zijn equivalent is met een minimale veelterm die volledig ontbindbaar is in onderling verschillende lineaire termen.
• Snelheidsvraagje: Waar of niet waar? Bespreek beide pijlen van de equivalentie.

"Zij R een ring met 1:

u en v hebben een inverse a.s.a. uv heeft een inverse"

En wat als de ring commutatief is?

Oefeningen

• Bewijs de stelling van Cauchy m.b.v. volledige inductie. (Zij G een groep met orde n, een veelvoud van een priemgetal p. Dan bestaat er een element in G dat orde p heeft. We bewijzen het met volledige inductie op $\alpha =n/p$
  • Bewijs de basistap, $\alpha =1$
  • Dan plaatste hij de inductiehypothese (geldt voor alle velden met kleinere $\alpha$) En vertelde hij dat we het uit het ongerijmde gingen bewijzen (veronderstel dat G geen element van orde p heeft). Ook plaatste hij hier dat we wisten dat G geen commutatieve groep was (uit de oefenzittingen).
  • Bewijs dat het aantal elementen van een niet triviale conjugatieklasse een veelvoud is van p
  • Bewijs dat het aantal elementen van Z(G) een veelvoud is van p
  • Beëindig je bewijs met een contradictie
• Zij $R=\mathbb{\mathbb{Z}}[X,Y]/(XY-1)$
  • Is $(\overline{1-X})$ een eenheid?
  • Is $(\bar{X})$ een maximale ideaal?
  • Bewijs dat R isomorf is met $\mathbb{\mathbb{Z}}[X,\frac{1}{X}]$. Hint: je mag hierbij veronderstellen dat elke $f\in \mathbb{\mathbb{Z}}[X,Y]$ te schrijven is als $f=\sum _{n\in \mathbb{\mathbb{Z}}}\sum _{\begin{array}{c}(i,j)\in I\\ j=i+n\end{array}}{a}_{ij}{X}^i{Y}^j$ met $I\subset {\mathbb{\mathbb{N}}}^2$ een eindig gebied.
  • Bepaal het breukenveld van R. (indien je c niet gemaakt had mocht je deze natuurlijk wel doen en c hierbij gebruiken)
• Zij $f=x^4+4x^2-2\in \mathbb{\mathbb{Z}}[X]$
  • bewijs dat f irreducibel is over $\mathbb{\mathbb{Q}}$
  • geef een ontbindingsveld $E\subset \mathbb{ℂ}$ over $\mathbb{\mathbb{Q}}$
  • bereken $[E:\mathbb{\mathbb{Q}}]$ (Deze laatste van de drie vraagjes was beduidend belangrijker dan de andere 2, en dit werd er ook bij gezegd)
• Een jordanvorm (6*6) (zonder parameters) Hierbij waren 4 verschillende hogere machten (vb ${(A-3I_6)}^3$ gegeven, waarvan er "minstens 1" nuttig was.

Eerste zit 2007-2008 Fysica, 15/01/2008

Theorie

• Factorisatiestelling (schriftelijk)
• Zij V een complexe vectorruimte en A een lineaire transformatie van V, op deze vectorruimte rust het hermitisch inprduct
  • gegeven: de decompositiestelling en een nuttig resultaat over minimale veeltermen en normale afbeeldingen A
  • Bewijs: A is normaal asa. Er een orthogonale basis van eigenvectoren van A bestaat
• Stelling van Bezout in een HID
• Snelheidsvraagjes: $\mathbb{ℝ}[X,Y]$, geef de grootste gemene deler van X en Y (ben het tweede vraagje vergeten vrees ik)
• Ander snelheidsvraagje: Zij F(q) een eindig veld met q elementen. Bekijk dan de additieve en multiplicatieve groepen F(q),+ en UF(q),. Welke zijn dan cyclisch?

Oefeningen

1

• Bewijs of geef een tegenvoorbeeld: Er bestaat geen groep van orde 8 met maar één element van orde 4
• Zij G een niet cyclische groep van orde 8 met precies twee elementen van orde 4, toon aan dat G isomorf is met ${{𝒟}}_4$

2

Waar of niet waar?(argumenten)

• $f:\mathbb{\mathbb{Z}}\to {\mathbb{\mathbb{Z}}}_6:x\to \overline{4x}$ is een goed gedefinieerd ringmorfisme
• $\frac{{\mathbb{\mathbb{Z}}}_2[X]}{(x^5+x^4+1)}$ is een veld

3

Bereken $[\mathbb{\mathbb{Q}}(\sqrt[4]{2008},\sqrt[6]{2008}):\mathbb{\mathbb{Q}}]$

4

Een jordanvorm

Tweede zit 2006-07, 30-08-07

Theorievragen

• Morfismestelling van groepen bewijzen (schriftelijk)
• Stelling van Kronecker
• A** = A
• Snelheidsvraagje: geef alle idealen van $\mathbb{\mathbb{Z}}$. en de priemidealen? en de maximale idealen?

Oefeningen

• een groep G, normaaldeler N en een deelgroep M die N omvat.
  • Bewijs dat: als $M/N\subset Z(G/N)$ dan $grp\{m*g*m^{-1}*g^{-1}\mid \mathrm{\forall }m\in M,\mathrm{\forall }g\in G\}\subset N$
  • als nu $M/N=Z(G/N)$ geldt dan dat $grp\{m*g*m^{-1}*g^{-1}\mid \mathrm{\forall }m\in M,\mathrm{\forall }g\in G\}=N$?? Bewijs of geef een tegenvoorbeeld
• Een ring $R,+,.$ heeft een priemideaal $P$ en twee idealen $A$ en $B$.

Bewijs dat als $A\cap B=P$ dat dan $A=P$ of $B=P$

• $\omega$ is de derde eenheidswortel en $\xi$ is de wortel van $2+\omega$.
  • a) Wat is de relatie tussen de velden $\mathbb{\mathbb{Q}}(\omega )$ en $\mathbb{\mathbb{Q}}(\xi )$.
  • b) Bereken $[\mathbb{\mathbb{Q}}(\xi ):\mathbb{\mathbb{Q}}]$
• Ne jordanvorm...

Eerste zit 2006-07, Fysica, 30-01-2007

Theorievragen

1. Zij $G$ een eindige groep en $a\in G$. Definieer $C_G(a)$ en $Cl(a)$. Bewijs dat $|Cl(a)|=\frac{|G|}{|C_G(a)|}$.
   1. Bijvraagje: Is $Cl(a)$ een deelgroep? en $C_G(a)$? Wat als $G$ niet eindig is?
2. Bewijs dat het aantal elementen van een eindig veld steeds ...(aanvullen en bewijzen)
3. Zij $V$ een $\mathbb{ℂ}$-vectorruimte en ${𝒜}$ een lineaire afbeelding.
   • Gegeven: We weten hoe decompositie van $V$ over ${𝒜}$ ineen zit.
   • Bewijs: ${𝒜}$ is diagonaliseerbaar asa de minimale veelterm van ${𝒜}$ ...(vul aan en bewijs)
4. Snelheidsvraagje:
   • Welke inclusies gelden er tussen ${\mathbb{𝔽}}_2$, ${\mathbb{𝔽}}_4$, ${\mathbb{𝔽}}_6$ en ${\mathbb{𝔽}}_8$?
   • Wat is ${\mathbb{𝔽}}_{16}\cap {\mathbb{𝔽}}_{64}=?$

Oefeningen

1. 1. Toon aan dat $G=\{\left(\begin{array}{cc}b& c\\ 0& d\end{array}\right)|b,d\in {\mathbb{\mathbb{Q}}}_0,c\in \mathbb{\mathbb{Q}}\}$ met de gewone matrixvermenigvuldiging een groep is.
   2. Toon aan dat $N=\{\left(\begin{array}{cc}1& a\\ 0& 1\end{array}\right)|a\in \mathbb{\mathbb{Q}}\}$ een normaaldeler is van $G$
   3. Met welke 'bekende' groep is $G/N$ isomorf?
2. Beschouw de ring $\mathbb{ℝ}[x,y]$.
   1. Geef een ideaal dat geen priemideaal is, en leg uit waarom.
   2. Geef een maximaal ideaal en toon dat aan.
3. 1. Toon aan dat $\sqrt[3]{5}\in ̸\mathbb{\mathbb{Q}}(\sqrt[3]{2})$ door het probleem te herleiden tot de oplosbaarheid van een stelsel in $\mathbb{\mathbb{Q}}$. (Hint: Een stelsel moet niet lineair zijn.)
   2. Wat is $[\mathbb{\mathbb{Q}}(\sqrt[3]{2},\sqrt[3]{5}):\mathbb{\mathbb{Q}}]$?
   3. Geef een basis van $\mathbb{\mathbb{Q}}(\sqrt[3]{2},\sqrt[3]{5})$ over $\mathbb{\mathbb{Q}}$
4. Stel $A=\left(\begin{array}{ccc}2& 1& -1\\ 3& 4& 1\\ 3& 2& 3\end{array}\right)$

   Zoek een inverteerbare matrix P en een Jordanmatrix J zodat $P^{-1}AP=J$.

Eerste zit 2006-07, Wiskunde, 15-01-2007

Theorievragen

1. Zij $\sigma \in {𝒮}$. Geef en bewijs de formule voor de orde van $\sigma$ in ${𝒮},\circ$ in termen van de disjuncte cykelschrijfwijze van $\sigma$.
   1. Bijvraagje: wat is de grootst mogelijke orde van een element in ${{𝒮}}_8$?
2. Zij R een HID en $x\in R$ met $x\ne 0$ en x geen eenheid. Bewijs dat x te schrijven is als een product van irreducibele elementen.

   Hints:

   • Een contradictie.
   • Een stijgende keten van idealen kan nuttig zijn.
3. Zij $K\subset E$ een velduitbreiding en $a,b\in E$ algebraïsch over K.
   1. Bewijs dat a+b algebraïsch is over K.
   2. Waar of niet? Zij $c,d\in E$ transcendent over K, dan is c+d transcendent over K.
4. Snelheidsvraagje: geef de maximale idealen in $\mathbb{ℂ}[X]$.

Oefeningen

1. Definitie: Zij G,* een groep en zij H een deelgroep van G. Het aantal linkse nevenklassen van H in G noemen we de index van H in G. De index van H in G is dus een van 0 verschillend natuurlijk getal of oneindig.
   1. Zij G,* een groep. Zij H een deelgroep in G met eindige index in G en zij $g\in G$. Toon aan dat de deelgroep $gH{g}^{-1}$ ook eindige index heeft in G.
   2. Zij G,* een groep en D de doorsnede van alle deelgroepen van G met eindige index in G. Toon aan dat D een normaaldeler is van G. Waarom is dit triviaal als G een eindige groep is?
   3. Geef een voorbeeld van een oneindige groep G,* waarvoor $\{e_G\}$ de doorsnede is van alle deelgroepen van eindige index in G.
2. Zij R,+,. een ring en zij I het ideaal voortgebracht door $\{ab-ba|a,b\in R\}$. Zij J een ideaal van R. Toon aan dat R/J commutatief is als en slechts als $I\subset J$.
3. Zij $\omega$ de primitieve derde eenheidswortel in $\mathbb{ℂ}$.
   1. Bepaal de relaties tussen de velden $\mathbb{\mathbb{Q}}(\sqrt{3}\omega )$, $\mathbb{\mathbb{Q}}(\sqrt{3}+\omega )$ en $\mathbb{\mathbb{Q}}(\sqrt{3},\omega )$.
   2. Bereken de uitbreidingsgraad $[\mathbb{\mathbb{Q}}(\sqrt{3},\omega ):\mathbb{\mathbb{Q}}]$.
   3. Bepaal een minimale veelterm van $\sqrt{3}+\omega$ over $\mathbb{\mathbb{Q}}$.
4. Stel $A=\left(\begin{array}{cccc}0& 1& 2& 0\\ -2& 4& 1& 0\\ -2& 1& 4& 0\\ -2& 0& 3& 3\end{array}\right)$

   Zoek een inverteerbare matrix P en een Jordanmatrix J zodat $P^{-1}AP=J$.

Eerste zit 2005-06, Wiskunde

Theorievragen

1. Zij G een groep en zij N een normaaldeler van G. Bewijs dat er een bijectie bestaat tussen de normaaldelers van G die N omvatten en de normaaldelers van G/N. Je mag hierbij het enkel feit gebruiken dat het beeld en het inverse beeld van een deelgroep onder een groepsmorfisme weer een deelgroep is. Al de rest moet bewezen worden.
2. Veronderstel dat R een hoofdideaaldomein is, en zij r een irreducibel element in R. Bewijs dat (r) dan een maximaal ideaal van R is. Geef ook een voorbeeld van een ring R, commutatief en met eenheidselement, en een irreducibel element r in R, zodat (r) geen maximaal ideaal van R is.
3. Bewijs de stelling van Kronecker: "Zij K een veld en zij f een niet-constante veelterm in K[X], dan heeft f een wortel in een velduitbreiding van K."

Snelheidsvragen

(Dit zijn de verraderlijke vraagjes die Veys op het mondeling examen stelt en die je *niet* mag voorbereiden, je krijgt er ongeveer 1 minuut tijd voor. Vaak zit er een addertje onder het gras. Wees dus niet te "snel".)

• Bestaat er een algebraïsch gesloten veld dat $\mathbb{ℂ}$ strikt omvat?
• Waar of fout? "Een groep is eindig als en slechts als alle elementen eindige orde hebben."

Oefeningen

1. Zij G een groep met precies twee niet-triviale deelgroepen.
   1. Bewijs dat G cyclisch is.
   2. Bewijs dat de orde van G van de vorm p³ of pq is, voor zekere priemgetallen p en q.
2. Met welke "bekende" ring is $\frac{{\mathbb{\mathbb{Z}}}_5[X,Y]}{(Y-X^2,XY+Y+2)}$ isomorf? Bewijs je antwoord.
3. Zijn $F\subset E$ velden. De Galoisgroep Gal(E, F) van E en F wordt gedefinieerd als de groep van alle veldautomorfismen $\sigma :E\to E$ (met andere woorden, ringautomorfismen van E waarvoor geldt dat $\sigma (1)=1$) die voldoen aan $\sigma (f)=f$, voor alle f in F. (Hierbij is de groepsbewerking samenstelling van afbeeldingen.) Toon aan dat $\text{<mrow data-mjx-texclass="ORD">Gal</mrow>}(\mathbb{\mathbb{Q}}(\sqrt{2}),\mathbb{\mathbb{Q}})\cong {\mathbb{\mathbb{Z}}}_2$.
4. 1. Kies een voorstelling van ${\mathbb{𝔽}}_8$ als ${\mathbb{𝔽}}_2\left[X\right]/(f)$, met $f\in {\mathbb{𝔽}}_2[X]$ een irreducibele veelterm van graad 3. Bepaal een basis van ${\mathbb{𝔽}}_8$ als ${\mathbb{𝔽}}_2$-vectorruimte. Toon aan dat het Frobeniusmorfisme $\phi :{\mathbb{𝔽}}_8\to {\mathbb{𝔽}}_8:x\mapsto x^2$ een lineaire transformatie van ${\mathbb{𝔽}}_8$ is, bepaal de matrix van $\phi$ ten opzichte van de gekozen basis, en bepaal de minimale veelterm van $\phi$.
   2. Zij p een priemgetal, en zij r een natuurlijk getal verschillend van 0. Laat zien dat het Frobenius-morfisme $\phi :{\mathbb{𝔽}}_{p^r}\to {\mathbb{𝔽}}_{p^r}:x\mapsto x^p$ een lineaire transformatie is van ${\mathbb{𝔽}}_{p^r}$ als vectorruimte over ${\mathbb{𝔽}}_p$. Zoek de minimale veelterm van $\phi$ en bewijs je vermoeden.

Eerste zit 2005-06, Fysica

Theorievragen

1. Zij G een groep, zij K een deelgroep van G en zij N een normaaldeler van G. Bewijs: $KN=\text{<mrow data-mjx-texclass="ORD">grp</mrow>}(K\cup N)$.
2. Zij $R,+,\cdot$ een ring. Bewijs dat de bewerking $*$ op R/N, gegeven door $(x+N)*(y+N)=x\cdot y+N$, goed gedefinieerd is als en slechts als N een ideaal is van R.
3. Bewijs dat "algebraïsch zijn van velduitbreidingen" transitief is. Is "transcendent zijn" dat ook?

Oefeningen

1. 1. Zij H een deelgroep van ${{𝒮}}_n$. Toon aan dat H een normaaldeler is als en slechts als voor elke $\sigma$ in H geldt dat alle elementen van ${{𝒮}}_n$ met dezelfde disjuncte cykel-schrijfwijze ook tot H behoren.
   2. Bewijs nu dat ${{𝒮}}_4$ een unieke deelgroep van orde 12 heeft.
2. Zij $R,+,\cdot$ een ring en definieer het centrum van R als $Z(R)=\{x\in R|\mathrm{\forall }a\in R:ax=xa\}$. We hebben in de oefenzittingen gezien dat Z(R) een deelring is van R.
   1. Toon aan dat Z(R) geen ideaal van R moet zijn.
   2. Het quotiënt R/Z(R) hoeft dus geen ringstructuur te hebben, maar in ieder geval wel een additieve groepsstructuur. Bewijs: als R/Z(R) een additieve cylische groep is, dan is R commutatief.
3. Definieer ${{𝒩}}_r^p$ als het aantal monische irreducibele polynomen van graad r over ${\mathbb{\mathbb{Z}}}_p$. Bewijs de volgende recursieformule: ${{𝒩}}_r^p=\frac{1}{r}(p^r-\sum _{d|r,d\ne r}d{{𝒩}}_d^p).$
4. 1. Zij $A:{\mathbb{ℝ}}^2\to {\mathbb{ℝ}}^2$ een lineaire afbeelding met karakteristieke veelterm $f_A(X)=X^2+aX+b$, en stel dat $a^2<4b$. Toon aan dat er een basis van ${\mathbb{ℝ}}^2$ bestaat zodat de matrix van A ten opzichte van die basis van de volgende vorm is: $\left(\begin{array}{cc}0& -b\\ 1& -a\end{array}\right)$
   2. Zij B de volgende 4 x 4 - matrix over de complexe getallen: $\left(\begin{array}{cccc}2& 1& 0& -1\\ 0& 3& 0& 0\\ -3& 1& 1& -5\\ 1& -1& 0& 4\end{array}\right)$

      Bepaal de Jordanvorm J van B en vind een matrix P zodat $P^{-1}BP=J$.

Eerste zit 2003-2004, Wiskunde

De theorievragen zijn verloren gegaan.

Oefeningen

1. Zij $G$ een groep en zij A een normaaldeler van G. Stel dat A commutatief is.
   1. Toon aan dat $\sigma :\frac{G}{A}\times A\to A:(gA,a)\mapsto ga{g}^{-1}$ een goed gedefinieerde groepsactie is van $\frac{G}{A}$ op $A$.
   2. Bepaal $Or(a)$ en $St(a)$ voor elke $a\in A$.
2. Zij $F$ een veld en beschouw de ring $F[[X]],+,\cdot$ zoals gedefinieerd in de oefeningenbundel. Herinner u dat de eenheden in deze ring de formele machtreeksen zijn waarvan de constante term verschillend is van 0. Beschouw de volgende uitspraken:
   • Het element $X$ is, op een eenheid na, het enige irreducibele element in deze ring.
   • De ring is een UFD.
   • De ring is een HID.

   Welke uitspraken zijn juist, welke zijn fout? Bewijs je antwoorden.

3. Zijn $F,E,K,L$ velden zodat $F\subset K\subset E$ en $F\subset L\subset E$. Noteer met $K\cdot L$ het kleinste deelveld van $E$ dat $K$ en $L$ omvat. Stel dat $[K\cdot L:F]$ eindig is.
   1. Toon aan dat $[K\cdot L:L]\le [K:F]$.
   2. Stel dat $[K:F]=2$ en $K\subseteq ̸L$. Bewijs dat gelijkheid optreedt in a).
   3. Stel dat $[L:F]=2$ en $L\subseteq ̸K$. Bewijs dat gelijkheid optreedt in a).
4. Beschouw de volgende matrix $A$ over $\mathbb{ℂ}$ (met $a\in \mathbb{ℂ}$ een parameter): $A=\left(\begin{array}{cccc}2& a^2-1& 0& -1\\ 0& 2& a^2-3a+2& 0\\ 0& 0& 2& 1\\ 0& 0& 0& a\end{array}\right)$

   Wat zijn de mogelijke Jordanvormen van $A$ over $\mathbb{ℂ}$?

Tweede zit 2004-2005, Wiskunde

De theorievragen zijn verloren gegaan.

Oefeningen

1. Zij $G$ een groep en zijn $M,N$ normaaldelers van $G$ met $M\subset N$. Stel dat $G/N$ cyclisch is en dat $|N/M|=2$.
   Toon aan dat $G/M$ commutatief is.
2. Beoordeel de volgende redenering: is de redenering juist? Is de redenering fout? Waarom?

   "Zij $R$ een ring met $1_R\ne 0_R$. Omdat $R$ een groep is voor de optelling en $1\in R$, bestaat er een invers element $-1_R$ van $1_R$. Omdat $(-1_R)(-1_R)=1_R$, is $-1_R$ een eenheid. Bijgevolg is $\left|R^{\times }\right|\ge 2$."

3. Een ring $R$ is Artins als elke dalende keten $I_0\supseteq I_1\supseteq I_2\supseteq \cdots$ van idealen stabiliseert (met andere woorden, als $I_n=I_{n+1}=I_{n+2}=\cdots$ voor een zeker natuurlijk getal $n$).
   1. Toon aan dat $\mathbb{\mathbb{Z}},+,\cdot$ geen Artinse ring is.
   2. Bewijs nu dat de quotiëntring $\mathbb{\mathbb{Q}}[X]/(X^3),+,\cdot$ wel een Artinse ring is.
4. Zij $E$ een veld met $\mathbb{\mathbb{Q}}\subset E\subset \mathbb{ℂ}$ en $[E:\mathbb{\mathbb{Q}}]=2$. Bewijs dat $E=\mathbb{\mathbb{Q}}(\sqrt{d})$ voor een zekere $d\in \mathbb{\mathbb{Z}}$.
5. Stel dat de matrix van een lineaire afbeelding $f:{\mathbb{ℂ}}^3\to {\mathbb{ℂ}}^3$ ten opzichte van een goede basis $\{e_1,e_2,e_3\}$ de volgende Jordanmatrix is: $\left(\begin{array}{ccc}2& 0& 0\\ 1& 2& 0\\ 0& 0& 2\end{array}\right)$. We kunnen ${\mathbb{ℂ}}^3$ natuurlijk ook als 6-dimensionale reële vectorruimte bekijken. Welke basis van ${\mathbb{ℂ}}^3$ kan je kiezen zodat $f$ ten opzichte van die basis in zijn Jordanvorm staat, en wat is die Jordanvorm?

Eerste zit 2004-2005, Fysica

(In 2004-2005 moesten de studenten Fysica de leerstof over velden niet kennen.)

Theorie

1. Zij $R$ een commutatieve ring met een eenheidselement en zij $I$ een ideaal van $R$. Bewijs dat $R/I$ een veld is als en slechts als $I$ een maximaal ideaal is.
2. Zij $V$ een complexe vectorruimte. Bewijs dat een lineaire transformatie ${𝒜}$ van $V$ normaal is als en slechts als $V$ een orthonormale basis van eigenvectoren van ${𝒜}$ heeft. Je mag gebruiken dat de minimale veelterm van een normale transformatie splitst in lineaire factoren.
3. Zij $G$ een groep en zij $N$ een normaaldeler. Bewijs dat de afbeelding $*:G/N\to G/N:(x*N)*(y*N)=(x*y)*N$ goed gedefinieerd is.

Oefeningen

1. 1. Bewijs dat er slechts één groepsmorfisme $\varphi :\mathbb{\mathbb{Q}}/\mathbb{\mathbb{Z}},+\to \mathbb{\mathbb{Q}},+$ bestaat.
   2. Bewijs dat er oneindig veel groepsmorfismen $\varphi :\mathbb{\mathbb{Q}},+\to \mathbb{\mathbb{Q}}/\mathbb{\mathbb{Z}},+$ bestaan.
2. Bewijs dat het aantal verschillende complexe $(n\times n)$-Jordanmatrices met slechts één eigenwaarde gelijk is aan het aantal conjugatieklassen van ${{𝒮}}_n$.
3. Een Euclidisch domein is een integriteitsdomein $R$, samen met een afbeelding $t:R\to \mathbb{\mathbb{N}}$ die voldoet aan
   • voor alle $a,b\in R$ (verschillend van 0) volgt uit $a\mid b$ dat $t(a)\le t(b)$, en
   • voor alle $a,b\in R$ (met $b$ verschillend van 0) bestaan er $r,q\in R$ zodat $a=bq+r$, met $r=0$ of $t(r)<t(b)$.

   Neem bijvoorbeeld $F[X]$ met $t:f\mapsto \mathrm{deg}f$.

   1. Zoek een ander voorbeeld van een Euclidisch domein.
   2. Bewijs dat een Euclidisch domein een hoofdideaaldomein is.
   3. Bewijs dat $t(u)=t(1)⟺u\in R^{\times }$.
4. Zij ${𝒜}:C_6\to C_6$ een nilpotente lineaire afbeelding met $\dim (\text{<mrow data-mjx-texclass="ORD">Ker</mrow>}{{𝒜}}^2)=4$. Bepaal de mogelijke waarden voor $\dim (\text{<mrow data-mjx-texclass="ORD">Ker</mrow>}{𝒜})$ en illustreer telkens met een voorbeeld.